明けましておめでとうございます。
本ブログは年が明けようが、年が戻ろうが平常運転でいきたいと思います。
今回は「行列」、なんともくるしかった微分よりははるかにPythonが使いやすそう。
行列
行列ってなんだっけ?
行列とかになってくると、もしかしたら学生時代に文系専攻の方とかだと全く触れたことがないということがあるかもしれません。
全くの未学習、でも機械学習の数学はちゃんと学びたいという場合は、おそらくここにかいてある程度だと不十分で、一度しっかりと学習する時間をとった方がいいのかもしれません。
行列の定義は以下のようなものです。
数や記号や式などを縦と横に矩形状に配列したものである。横に並んだ一筋を行、縦に並んだ一筋を列と呼ぶ。
引用元:行列 - Wikipedia
イメージ的には、以前扱ったベクトルの拡張版みたいなものでしょうか。
ベクトルの場合は縦か横どちらかの方向に延びていましたが、行列の場合は縦と横両方の要素を持ちます。
関係性的には「行列⊃ベクトル」ということができそうです。
一般的なソフトなどでは表現が非常に面倒ですが、具体的には以下のようなものになります。
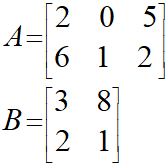
これが機械学習において、なんの役に立つのか?それはこれから一緒に学んでいきましょう。
でも、なんとなくニュートラルネットワークのそれっぽくないですか??
行列の加減算
やりながら段々思い出してきましたが、同じようなことをPythonの基本操作視点でやっていましたね。
行列の加減算自体はなんてことはなく、単純に同じ位置に存在する数字同士を加減すればいいだけです。
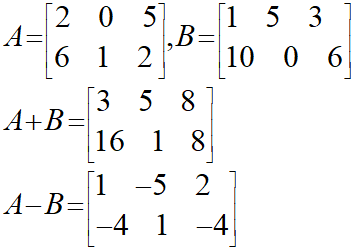
注意点をあえて挙げるとすれば、同じ位置に存在するもの同士を計算するので、行と列の次元が異なると計算できないということぐらいでしょうか。
以前にも扱いましたが復習がてらPythonで試してみます。
・例
import numpy as npy
# 行列の定義
A = npy.array([[2,0,5],[6,1,2]])
B = npy.array([[1,5,3],[10,0,6]])
add = A+B
sub = A-B
print("加算の結果")
print(add)
print("減算の結果")
print(sub)・出力結果
加算の結果 [[ 3 5 8] [16 1 8]] 減算の結果 [[ 1 -5 2] [-4 1 -4]]
numpyで行列をそれぞれ定義して、加減算を行って結果を出力する。これだけであれば非常に単純ですね。
スカラー倍
これも以前やった内容とかぶるのでかるく。
ベクトルや行列に対して、「2、-3、0.1」など単一のいわゆる普通の数字のことをスカラーというのでした。
つまりスカラー倍というのは、行列に対してそれらの普通の数字を掛けることを指します。
これに関しても、各要素に数字を掛けていけばいいだけなので、極めて普通の感覚で進めることができるのではないでしょうか。
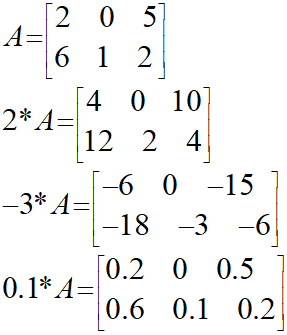
Pythonも復習ですね。
・例
import numpy as npy
# 行列の定義
A = npy.array([[2,0,5],[6,1,2]])
result1 = 2*A
result2 = -3*A
result3 = 0.1*A
print("2倍")
print(result1)
print("-3倍")
print(result2)
print("0.1倍")
print(result3)・出力結果
2倍 [[ 4 0 10] [12 2 4]] -3倍 [[ -6 0 -15] [-18 -3 -6]] 0.1倍 [[0.2 0. 0.5] [0.6 0.1 0.2]]
行列の乗算
掛け算ですね。行列の乗算に関しては加減算と少し感じが変わってきます。
行列の乗算自体を知っている方はどのようにPythonで表現するのかをそれも知っている方は特に学ぶことはないです。
※とは言いつつ、行列の乗算自体もしれっと過去記事でやってはいます。
で、どう計算するのかというと、まずはベクトル様の行列の乗算からいきます。
横ベクトルのAと縦ベクトルのBが存在するとき、「A×B」及び「B×A」は以下のように計算されます。

横方向の要素を一つのまとまりと捉えて、対応する縦要素と掛け合わせ総和するって感じでしょうか。
※言葉で表現するのが非常に難しいですね。
このことから以下の2点の特徴が分かります。
・掛ける順番によって解が変わる
・横と縦の要素数が異なる行列(ベクトル)同士では乗算できない
今回はベクトルとして扱っていますが、行列でやっても同じことが言えます。
Pythonでの実装は以前も扱いましたが、「dot」を用いて行います。
・例
import numpy as npy
# 行列の定義
A = npy.array([[2,0,5]])
B = npy.array([[3],[2],[-1]])
result1 = A.dot(B)
result2 = B.dot(A)
print("A×Bの解")
print(result1)
print("B×Aの解")
print(result2)・出力結果
A×Bの解 [[1]] B×Aの解 [[ 6 0 15] [ 4 0 10] [-2 0 -5]]
そして本題の行列に入ります。
ベクトルで考えた場合のB×Aの感覚がしっくりきていれば特に問題ないでしょう。
基本はベクトルと同じように計算を行います。
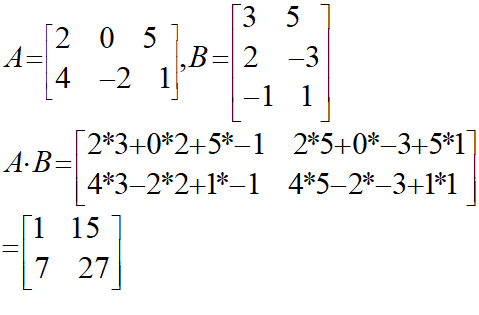
※もちろんこの場合も「B×A」という乗算はできますが、しんどいので割愛。Pythonにまかせます。
Pythonにおける実装もベクトルと同じ要領でOKです。
・例
import numpy as npy
# ベクトルの定義
A = npy.array([[2,0,5],[4,-2,1]])
B = npy.array([[3,5],[2,-3],[-1,1]])
result1 = A.dot(B)
result2 = B.dot(A)
print("A×Bの解")
print(result1)
print("B×Aの解")
print(result2)・出力結果
A×Bの解 [[ 1 15] [ 7 27]] B×Aの解 [[ 26 -10 20] [ -8 6 7] [ 2 -2 -4]]
いまいちしっくりこない場合は行列の乗算は特殊!と思っていおいて、実際に必要になったときにしっかり理解する。でなんとかなるのかな???
長くなりそうなので一旦きります。
・今回のソース
python_dev/Python_math4.ipynb at master · wantanblog/python_dev · GitHub