前回は分類の問題に対してニューラルネットワークモデルをPythonで実装することによって解決しようとしました。
また、重みを求める際には数値微分法によって求めましたが、求めた重みは近似値であり算出にそれなりのコストがかかりました。
今回は同じくニューラルネットワークモデルに関する実装で、誤差逆伝搬法について学んでいきます。
考える問題は前回までと同じです。
www.wantanblog.com
誤差逆伝搬法(バックプロパゲーション)
誤差逆伝搬法とは
あまりなじみがありませんでしたが、ニューラルネットワークで重みを求める手法としては一般的な手法なようです。
誤差逆伝搬法ではニューラルネットワークの出力値と正解との誤差を出し、出力層の重みを調整し、そこから中間層へと逆方向に重みを更新していく手法です。

これだけでは逆方向に計算が進んでいくということ以外いまいちイメージが湧きませんのでこれから少し細かく見ていきます。
内部の仕組み的な話がしばらく続きます。
平均交差エントロピー誤差を定義
今回の問題ではクラスの分類を扱っていますので、「ニューラルネットワークの出力値と正解との誤差」を平均交差エントロピー誤差で表現します。
・平均交差エントロピー誤差
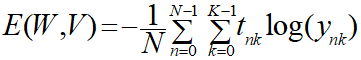
平均交差エントロピー誤差はそもそもデータごとの誤差を出してその平均を算出しているものですので、データごと(n)の誤差を考えます。
以下の式を個別交差エントロピー誤差と仮称します。
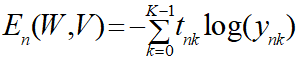
そうすると、平均交差エントロピー誤差は個別交差エントロピー誤差を用いて以下のように表現できます。
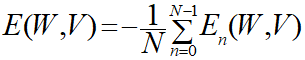
勾配法では平均交差エントロピー誤差の偏微分式を必要としますので、個別交差エントロピー誤差の偏微分式(∂En/∂wij)を導出してそこから本来求めたい偏微分式(∂E/∂wij)を求めるというアプローチになります。
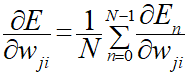
出力層の偏微分式を求める
誤差逆伝搬法では出力層の重み(v)から求めていきます。
出力層のエントロピー誤差を重みで偏微分した式(∂E/∂v)を連鎖律により分解します。

∂E/∂aの導出
まずは∂E/∂aから見ていきます。
Eは先ほど示したΣを使用した式で表現されるので以下のようにすることができます。
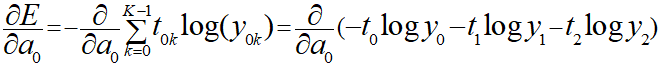
上記の式では入力総和aから見て、正解であるtは入力総和とは関係ないので定数とみなせます。
一方yは入力総和から算出される出力値なので、当然相関があるため偏微分はこちらにかかり以下のように式を展開することができます。
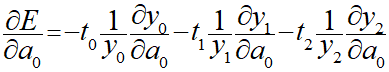
対数の微分はこちらも連鎖律を使い以下のように導出しました。
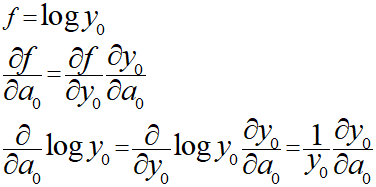
式上のyは出力層のソフトマックス関数なので、以下の公式を適用して一番目の項を変形します。
・ソフトマックス関数の微分
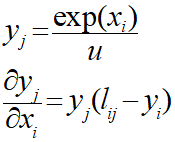
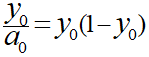
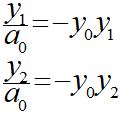
上記から∂E/∂aを導出していきます。
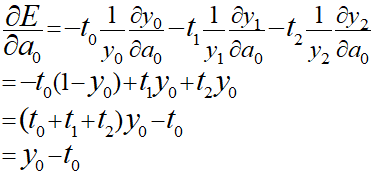
tはクラス分類を表すのでt0、t1、t2のどれかが1で他は0となるので総和すると必ず1になるため省略することができます。
ここまではk=0の場合で求めていますので、同様にk=1、2の場合も求めると以下のようになります。
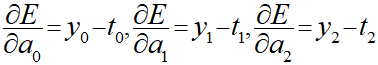
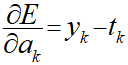
∂a/∂vの導出
次に連鎖律で分解した右側部分の∂a/∂vについて導出していきます。
入力総和aをk=0の場合で考えていきます。
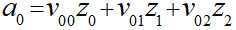
前と同じような形で偏微分を考えていくと、変数が項ごとに分かれているので偏微分の他の項が消えるため考えやすいです。
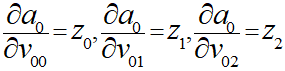
上記より、以下のようにまとめることができます。
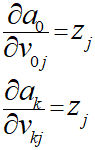
∂E/∂vの導出
これまでの導出した式を利用することで∂E/∂vを表現することができます。
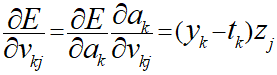
更新規則の導出
∂E/∂vとはなんだったかと言うと、勾配法における今の地点から次の地点に移動するための更新規則でした。
なので、勾配法の更新規則は以下のように表現できることになります。
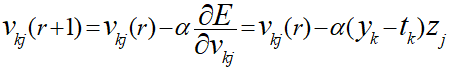
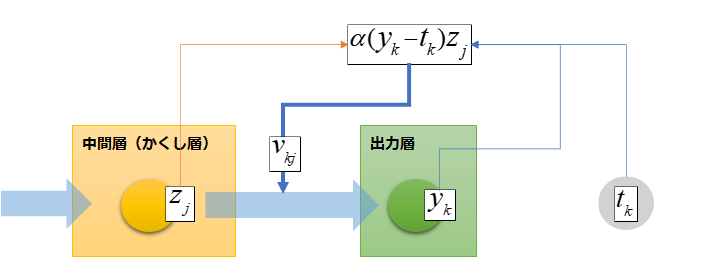
このことから正解(t)と出力値(y)の差分が重みにかかるので、値が正解に近づくほど変化が小さくなり、正解と出力値が同じになると変化がなくなるということが分かります。
また中間層の出力値(z)の値が大きければ大きいほど、その結合からの重みvへの寄与が大きくなり変更量も大きくなるということが分かります。
中間層の偏微分式を求める
出力層の偏微分式が導出できたので、次に中間層の偏微分式を導出することによって学習則を求めます。
こちらも出力層と同様に誤差Eを重みwで偏微分して連鎖律によって求めていきます。
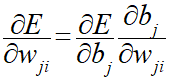
∂E/∂bの導出
まずは前半部分から求めていきます。
∂E/∂bを展開すると以下の式になります。
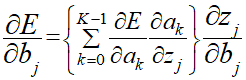
ぱっと見で意味が分かったでしょうか?私はわかりませんでした。
これぐらいはわかるようにならないといけないのかなぁ・・
ちょっと脱線して少し詳しく見ていきます。
一目で分かるなら飛ばしてOK。
入力総和bと入力総和aは全体でみると以下のような関係になっています。
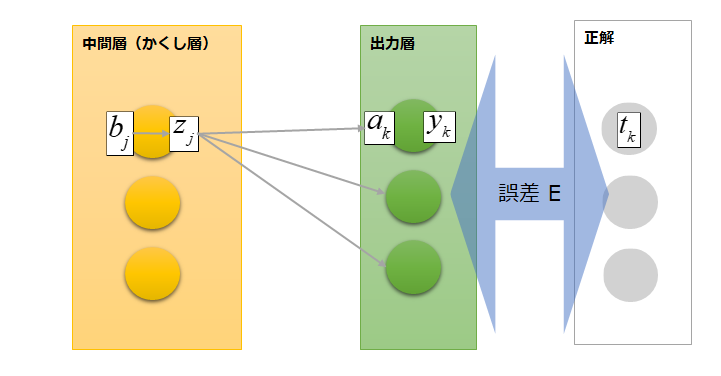
入力総和bjは入力総和aの各ニューロンに関与しているため、出力層の各ニューロンと正解の誤差を表すEを表現する際には入力総和aは各ニューロンの総和を求める必要があるのです。
上記の図だけだと、b(z)も総和を求める必要がありそうに見えますが、今は偏微分を考えているため中間層のほかのニューロンは定数として考えることができるので総和を求める必要がありません。
最近は気軽に連鎖律を使用していますが、連鎖律はそもそも入れ子関数の場合に使える規則です。
なので、関数の形で表すと以下のように表現することができます。
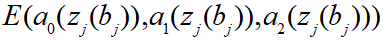
本筋に戻ります。
上記のように展開すると、∂E/∂aの部分は先に導出した以下の式で置き換えることができます。
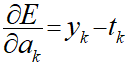
次に∂a/∂zの部分ですが、以下のように表現できます。
ここも分かりにくかったですが、入力総和aを求めるためにvzの総和を求めます。
その後、vjの偏微分を行うことによってj番目以外の項が消え、j番目の項は微分が行われるためvだけが残ることになります。
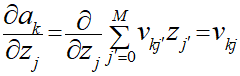
最後に∂z/∂bの部分ですが、zは中間層の出力値なので、中間層の活性化関数(今回はシグモイド関数)を用いることによって、bで式を表すことができます。
今の段階では複雑化を避けるため、活性化関数h()で以下のように表現しておきます。
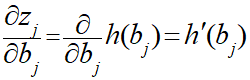
最終的に∂E/∂bは以下のように表現できます。
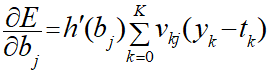
この式は出力層の各ニューロンの出力値と重みv、中間層の入力総和から成っているのでこの辺が誤差逆伝搬と言われる所以だそうです。
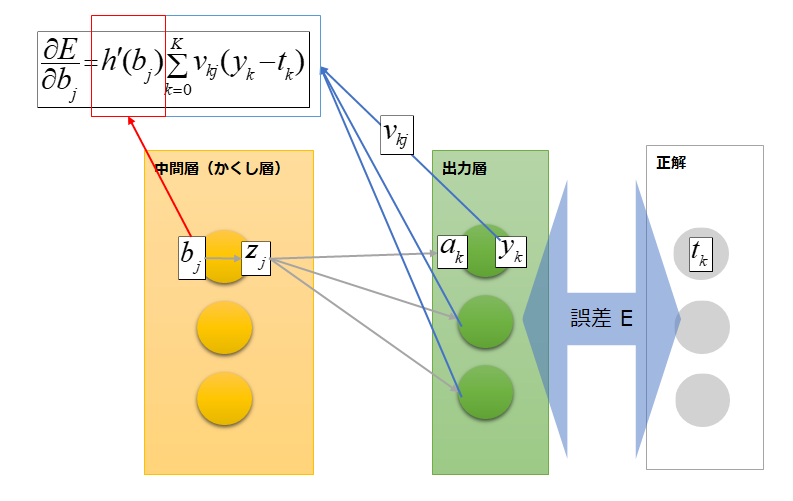
とりあえずちょー大変。
∂b/∂wの導出
先ほども似た考え方が出てきました。
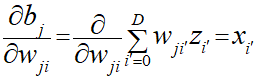
bは入力総和なので、入力値xと重みvをかけたものの総和になります。
それをwで偏微分するとji番目以外の項は定数とみなせるので消すことができ、ji番目の項はwjiで微分するためxのみが残るというわけです。
こっちは簡単!
∂E/∂wの導出
こちらも同じく、導出した式を利用することで∂E/∂wを表現することができます。
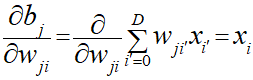
更新規則の導出
勾配法における今の地点から次の地点に移動するための更新規則となるのである重みwから次の重みへの変化を以下のように表現できます。
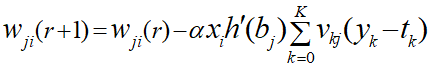
最終的に以下のようなイメージになりました。
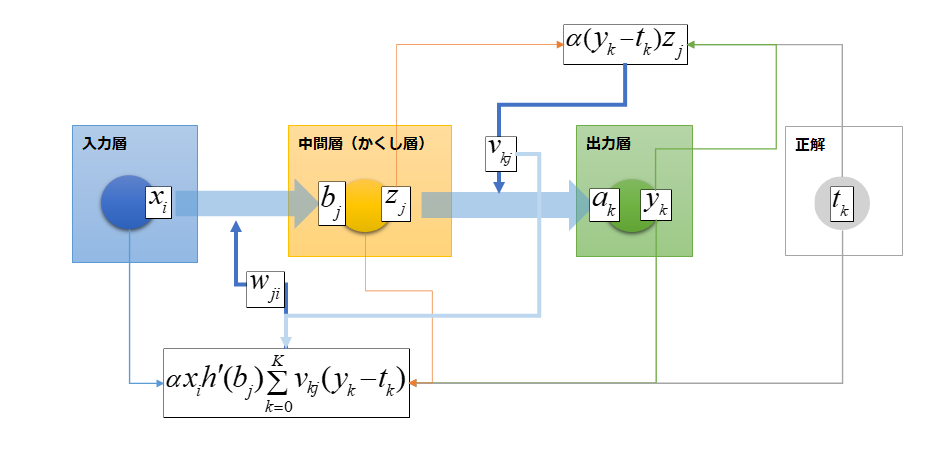
逆伝播している様子がなんとなくついたかなという感じ。
今回ここまででは、N個の入力データの一つに対して求めているので実際に実装する際にはN個分の平均をとります。
今回は2層フィードフォワードネットワークに関して求めてきましたが、層がいくつに増えても考え方はもちろん、式の形も基本的には同じとのこと。
実装は次回にします。