【Python】入門⑤ Pythonでグラフを扱う その１（二次元グラフの描写）

機械学習プログラミングをしっかりとやろうと思った場合、数学的な知識に加えてグラフの扱いが必須となります。
※数学系の参考書を読んで思っただけです。

今回はJupyter Notebookでのグラフ描写を扱います。プログラミングでグラフを扱うのは全くの初めてなのでどんな感じになるのか全くわかりませんね。

２次元のグラフ

まずはとにかくグラフを描いてみる

Pythonでグラフを描写するには、「matplotlib.pyplot」を利用します。
X軸とY軸に当たる配列を設定して、グラフを描写するようです。

説明だけではイメージが付きにくいのさっそく使っていきましょう。

・例

# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline

# X軸に0から9までの配列
xline = npy.arange(10)
# Y軸にランダム値の配列
yline = npy.random.rand(10)

# pltに要素を設定する
plt.plot(xline, yline)
# グラフを描写する
plt.show()

・出力結果

これだと簡単すぎるグラフですけど、あーなんかそれっぽいですね。
今回はランダム値を使ってるので実行ごとに出力結果が変わります。

次に進む前に少し遊んでみます。

【指数関数のグラフ】

自然対数を使った以下の指数関数をグラフ描写してみます。

y = e^x

自然対数には以前の記事で紹介した「npy.exp」を使用します。

・例

# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline

# X軸に0から9までの配列
xline = npy.arange(10)
# 指数関数化
yline = npy.exp(xline)

# pltに要素を設定する
plt.plot(xline, yline)
# グラフを描写する
plt.show()

・出力結果

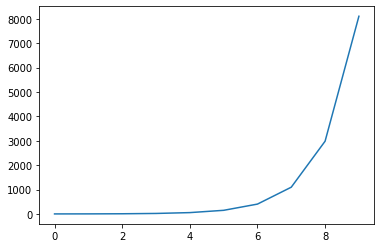
それっぽい！！

三次関数

二次関数のグラフ描写もままならないままにですが、三次関数のグラフを描写してみます。

関数は以下を題材としたいと思います。

f(x) = x(x - 1)(x + 2)　　　・・・式（１）

関数の定義についてですが、ここで「数学の関数」と「プログラミングの関数」が一致します。
つまりは関数に式（１）を定義するということです。

・例

def f(x):
    return x*(x-1)*(x+2)

result1 = f(1)
result2 = f(2)
print("result1 = " + str(result1))
print("result2 = " + str(result2))

・出力結果

result1 = 0
result2 = 8

式（１）では「f(1) = 0」、「f(2) = 2*1*4 = 8」なので確かによさそうです。

では実際にグラフを描写してみます。
ちなみに関数の引数に配列を渡した場合、戻り値も配列になるので、この辺はPythonっていうのはかなり柔軟なんですね。

・例

# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f(x):
    return x*(x-1)*(x+2)

# X軸に0から9までの配列
xline = npy.arange(-5,5)
yline = f(xline)

# pltに要素を設定する
plt.plot(xline, yline)
# グラフを描写する
plt.show()

・出力結果

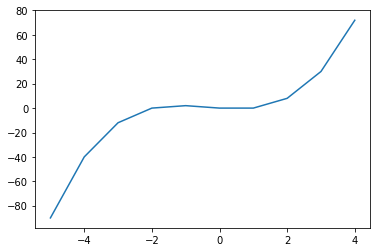
「x=-2」のとき極大値をとり、「x=1」のとき極小値をとるグラフなので、まぁ妥当だと思えますが、指数関数のときも思いましたが曲線だとグラフの形がやや歪なんですよね。
概形をつかむにはこれでも十分なんですけどね。

これは要素の数が少ないせいですね。

数学の授業とかで人間が描写する場合には、曲線になることを意識して描くので自然とそれっぽ形になりますが、正直すぎるコンピュータを描かせる場合にはxが整数の値のみをとっても不十分ということなんでしょう。

これを解消するために「arange」の代わりにNumpyの「linspace」を使用します。
「linspace」では第一、第二引数で範囲を指定し、第三引数でその範囲に打つポイントの数を指定します。

・例

# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f(x):
    return x*(x-1)*(x+2)

# X軸に0から9までの配列
xline = npy.linspace(-5,5,20)
yline = f(xline)

print("参考："+ str(xline))
# pltに要素を設定する
plt.plot(xline, yline)
# グラフを描写する
plt.show()

・出力結果

参考：[-5.         -4.47368421 -3.94736842 -3.42105263 -2.89473684 -2.36842105
 -1.84210526 -1.31578947 -0.78947368 -0.26315789  0.26315789  0.78947368
  1.31578947  1.84210526  2.36842105  2.89473684  3.42105263  3.94736842
  4.47368421  5.        ]

参考にポイントを打ったxの値を出力しています。
20点も打つとだいぶ滑らかな美しい曲線になりましたね。曲線グラフを描写する場合には使用必須かもしれません。

リンク