前回の2次元入力の続き。
データセットの準備
scikit-learn アヤメの品種データ
今回はデータセットに回帰のときにも使用した「scikit-learn」に用意されているデータの中のアヤメの品種データ(Iris plants dataset)を使用する。
※3クラスの分類に使用できるデータの準備がすぐには難しかったため。
取得できるデータは以下の通り。
■説明変数
| 0 | sepal length (cm) | がく片の長さ |
|---|---|---|
| 1 | sepal width (cm) | がく片の幅 |
| 2 | petal length (cm) | 花弁の長さ |
| 3 | petal width (cm) | 花弁の幅 |
■目的変数
目的変数に格納されているデータはそれぞれ以下を表しています。
| 0 | setosa(ヒオウギアヤメ) |
|---|---|
| 1 | versicolor(ブルーフラッグ) |
| 2 | virginica(バージニカ) |
今回は入力を2次元としていますので、少々無理やりですが「がく片の長さ」と「がく片の幅」から3種(クラス)の分類に試みたいと思います。
データセットの準備
上記で述べたアヤメのデータを取得して今回の分類用に成形し設定します。
だいたいは前回記事の「2次元入力3クラス分類」と同じ実装です。
・データ準備の実装例
# データ準備
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
# アヤメ品種データの読み込み
from sklearn.datasets import load_iris
iris_data = load_iris()
# 説明変数
X_array = iris_data.data
# カラムデータを取得
X0=X_array[:,0]
X1=X_array[:,1]
# 目的変数
t_array = iris_data.target
T=t_array
N=len(X0)
petal_data=npy.zeros((N,2))
T3 = npy.zeros((N,3), dtype=npy.uint8)
#データの設定
for i in range(N):
# がく片データをまとめる
petal_data[i]=[X0[i], X1[i]]
# 0[1,0,0] 1[0,1,0] 2[0,0,1]
if T[i] == 0:
T3[i]=[1,0,0]
elif T[i] == 1:
T3[i]=[0,1,0]
else:
T3[i]=[0,0,1]
X_range0=[min(X0)*0.9,max(X0)*1.1]
X_range1=[min(X1)*0.9,max(X1)*1.1]
# データをclassdata3.npzファイルに保存する
npy.savez('classdata3.npz',X=petal_data,T3=T3,X_range0=X_range0,X_range1=X_range1,X_n=N)・データ設定の実装例
# データの設定
# データをclassdata3.npzファイルから取り出す
sample_data = npy.load('classdata3.npz')
# 入力値の設定
X=sample_data['X']
# クラス(答え)の設定
T3=sample_data['T3']
# がく片の長さの表示範囲設定
X_range0=sample_data['X_range0']
# がく片の幅の表示範囲設定
X_range1=sample_data['X_range1']
# データ数の設定
N=sample_data['X_n']今回のデータをプロットしておきます。
・実装例
# データプロットの表示
import matplotlib.pyplot as plt
%matplotlib inline
# データ表示
def show_data3(x,t):
wk,K = t.shape
c=[[.5,.5,.5],[1,1,1],[0,0,0]]
for k in range(K):
# 平日(クラスA)はグレー表示、休日(クラスB)は白抜き表示
plt.plot(x[t[:, k]==1,0],x[t[:, k]==1,1],linestyle='none',markeredgecolor='black',marker='o',color=c[k],alpha=0.8)
plt.grid(True)
plt.figure(figsize=(5,3))
plt.subplots_adjust(wspace=0.5)
show_data2(X, T3)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.show()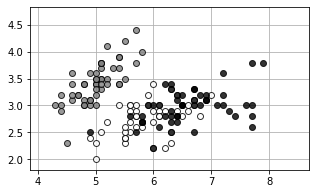
数学的な導出
ロジスティック回帰モデル
出力が3クラスになる場合なのでソフトマックス関数をモデルの出力を用います。
ソフトマックス関数は以下のような式です。

ソフトマックス関数については以下の記事でも扱いました。
まずは入力総和(a)から定義します。
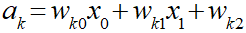
この入力総和をソフトマックス関数に適用します。
ソフトマックス関数の特徴としてはyの総計が「1」になります。
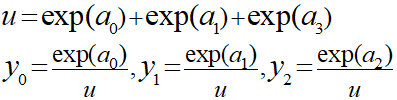
パラメータWは今回の例で入力総和から以下のように9つ設定します。
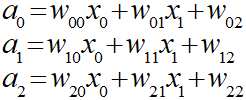
実際のプログラムなどでは数列で以下のように表現します。
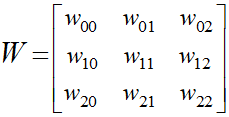
平均交差エントロピー誤差
今回も前回までと同じように入力データから目的変数が導き出される最も尤もらしい確率を求める最尤推定を行います。
そこでまずは尤度の表現を行います。
■尤度の表現
事象x(入力データ)が起きたときに、事象t(目的変数)が起きる確率は汎用的に以下のように表現できます。
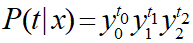
各「y」はクラス1~3が発生する確率を表しているので、クラス1の場合は「y0」のみが残るというようになります。
上記の式では事象の一つが発生する確率を表現しているので、全ての事象が発生した場合を求めるために乗算します。
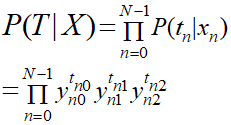
この状態では3つのyが乗算されている場合なので、ここも「Π」を用いた表現にすることでさらに汎用化します。
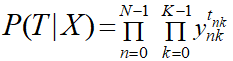
このように表現することで分類するクラス数が限られない表現を行うことができます。
■平均交差エントロピー誤差
上記の式から平均交差エントロピー誤差を導出します。
前回までにやっている通り、対数表現にして平均をとり値をマイナスにします。
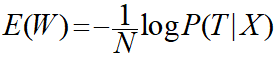
式を整理します。
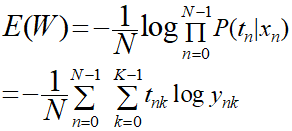
上記で得られた式を関数として定義します。
勾配法による解の導出
勾配法により最小値を求めるためには上記で得られた平均交差エントロピー誤差の式を偏微分します。
ソフトマックス関数の偏微分は以下のような公式を活用できます。
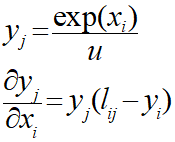
この公式を用いて平均交差エントロピー誤差の式を偏微分すると全ての「k」と「ⅰ」において以下のようになります。
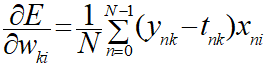
上記を偏微分式として定義します。
Pythonによる実装
実装の全容
これまで算出した式をPythonによって実装します。最初に全容を示します。
・3クラス分類における決定境界を求める実装
from scipy.optimize import minimize
# 3クラス分類ロジスティック回帰モデル
def logistic3(x0,x1,w):
K=3
w=w.reshape((3,3))
n = len(x1)
y = npy.zeros((n,K))
for k in range(K):
y[:, k] = npy.exp(w[k,0]*x0 + w[k,1]*x1+w[k,2])
wk = npy.sum(y,axis=1)
wk = y.T / wk
y = wk.T
return y
# 交差エントロピー誤差
def cee_logistic3(w,x,t):
X_n=x.shape[0]
y=logistic3(x[:,0],x[:,1],w)
cee = 0
N,K = y.shape
for n in range(N):
for k in range(K):
cee = cee -(t[n,k]*npy.log(y[n,k]))
cee = cee/X_n
return cee
# 交差エントロピー誤差の微分
def dcee_logistic3(w,x,t):
X_n=x.shape[0]
y=logistic3(x[:,0],x[:,1],w)
dcee = npy.zeros((3,3))
N,K = y.shape
for n in range(N):
for k in range(K):
dcee[k,:] = dcee[k,:] -(t[n,k]-y[n,k])*npy.r_[x[n,:],1]
dcee = dcee / X_n
return dcee.reshape(-1)
# パラメータサーチ
def fit_logistic3(w_init,x,t):
res = minimize(cee_logistic3,w_init,args=(x,t),jac=dcee_logistic3,method="CG")
return res.x
# 等高線表示
def show_contour_logistic3(w):
xn = 30
x0=npy.linspace(X_range0[0],X_range0[1],xn)
x1=npy.linspace(X_range1[0],X_range1[1],xn)
xx0,xx1 = npy.meshgrid(x0,x1)
y = npy.zeros((xn,xn,3))
for i in range(xn):
wk = logistic3(xx0[:,i],xx1[:,i],w)
for j in range(3):
y[:,i,j]=wk[:,j]
for j in range(3):
cont=plt.contour(xx0,xx1,y[:,:,j],levels=(0.5,0.7),colors=['cornflowerblue','k'])
cont.clabel(fmt='%.1f',fontsize=10)
plt.grid(True)
W_init = npy.zeros((3,3))
W_init = [[1,1,1],[1,1,1],[1,1,1]]
W=fit_logistic3(W_init,X,T3)
print(npy.round(W.reshape((3,3)),2))
cee = cee_logistic3(W,X,T3)
print("CEE={0:.2f}".format(cee))
plt.figure(figsize=(3,3))
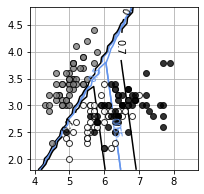
show_data3(X,T3)
show_contour_logistic3(W)
plt.show()・出力結果
[[-32.8 29.94 91.53]
[ 16.95 -13.67 -37.74]
[ 18.85 -13.27 -50.79]]
CEE=0.37
実装内容について軽くみていきます。
ロジスティック回帰モデル
# 3クラス分類ロジスティック回帰モデル
def logistic3(x0,x1,w):
K=3
w=w.reshape((3,3))
n = len(x1)
y = npy.zeros((n,K))
for k in range(K):
y[:, k] = npy.exp(w[k,0]*x0 + w[k,1]*x1+w[k,2])
wk = npy.sum(y,axis=1)
wk = y.T / wk
y = wk.T
return yソフトマックス関数の分子部分をループによって算出します。
入力パラメータであるWは3×3の配列なので、w0~w2までを三回ループします。
ループでy0~2までを求めた後に合計uを出して分母とすることによってソフトマックス関数の式とします。
平均交差エントロピー誤差
# 交差エントロピー誤差
def cee_logistic3(w,x,t):
X_n=x.shape[0]
y=logistic3(x[:,0],x[:,1],w)
cee = 0
N,K = y.shape
for n in range(N):
for k in range(K):
cee = cee -(t[n,k]*npy.log(y[n,k]))
cee = cee/X_n
return cee平均交差エントロピー誤差の式なので以下の式を実装しています。
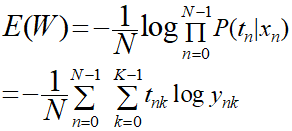
外のループがプロット数Nの分だけ繰り返して、内側のループは分類クラスの数Kだけ繰り返しを行い合計を算出します。
平均なのでなので最後にプロット数Nで割ることで平均交差エントロピー誤差(CEE)を算出しています。
交差エントロピー誤差の微分式
# 交差エントロピー誤差の微分
def dcee_logistic3(w,x,t):
X_n=x.shape[0]
y=logistic3(x[:,0],x[:,1],w)
dcee = npy.zeros((3,3))
N,K = y.shape
for n in range(N):
for k in range(K):
dcee[k,:] = dcee[k,:] -(t[n,k]-y[n,k])*npy.r_[x[n,:],1]
dcee = dcee / X_n
return dcee.reshape(-1)微分後の式なので、以下の式を実装しています。
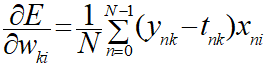
式の内容自体はそのままですが、戻り値としてはロジスティック回帰モデルの入力パラメータであるW(3×3)となります。
求めるのは後述する関数にまかせますが、各値の場合のWを求めて最適なものを算出することになります。
パラメータのサーチ
# パラメータサーチ
def fit_logistic3(w_init,x,t):
res = minimize(cee_logistic3,w_init,args=(x,t),jac=dcee_logistic3,method="CG")
return res.x前回も使用したminimize関数により最適な入力パラメータWを求めています。
出力結果について
出力結果を再掲します。
[[-32.8 29.94 91.53]
[ 16.95 -13.67 -37.74]
[ 18.85 -13.27 -50.79]]
CEE=0.37

最初に出力しているのがminimize関数によるによって算出した今回の最適パラメータWです。
このパラメータからCEE(平均交差エントロピー誤差)とグラフを求めています。
本来の問題を思い出します。
| クラス① | setosa(ヒオウギアヤメ) |
|---|---|
| クラス② | versicolor(ブルーフラッグ) |
| クラス③ | virginica(バージニカ) |
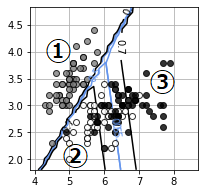
上記の分類だったので、クラス①については他の②③と明確な違いがあるため、グラフ上の0.7と0.5の間隔が狭くなっています。
※等高線が急になっているイメージ
クラス②と③についてはプロット数が多ければ違いはありますが、曖昧な領域が存在しているためグラフ上の0.7と0.5の間隔が広くなっています。
※等高線が緩くなっているイメージ
今回求めたかった決定境界は0.5(青線)になっている部分となり、ここを境にクラスの分類を行うことができます。
ーーーーーーーーーーー
今回はここまで。分類についてはややあっさりでしたが次回からはディープラーニングに入っていきます。
機械学習分野は難しくて進捗が芳しくない・・
・今回のソース
python_dev/Classification_2-2.ipynb at master · wantanblog/python_dev · GitHub