やっと次章に進みました。今回から機械学習の教師あり学習における「分類」を扱っていきます。
分類
機械学習の有名な手法には「回帰」と「分類」がありました。
「回帰」ではデータセットから関数などの導出により連続した値の予測を行いました。
「分類」ではデータセットから特定のデータをどのクラスに分類されるかを判定することになります。
具体的には、試験における点数を合格と不合格に分類する。画像を犬、猫を分類する。
回帰ではあくまで予測値を出力する関数でしたが、分類では確率の概念を取り込み不確かさを表現していきます。
問題設定
まずは分類を行うべき問題を設定します。
データセット準備
問題設定を行うためのデータを準備します。
今回は毎度おなじみの本ブログのGoogleアナリティクスのデータの中でアクセス数から平日、休日の分類を題材としたいと思います。
本ブログは、IT関連に特化させているため、平日と休日では明確にアクセス数に差があります。
※エンジニアが仕事中に検索しヒットしていることが多いと予測されるため
データセットの準備方法は以前行った回帰のときと同様です。
適切なデータを準備できない場合には乱数関数でランダムな値を準備すればよいでしょう。
・データセット例
# データセット準備
import numpy as npy
# データ生成
# ある月のアクセス数
views =[95,130,201,165,185,179,153,121,119,223,152,239,198,205,116,100,206,238,242,266,183,122,124,201,203,248,223,207,123]
# 1=休日、0=平日
day_of_week=[1,1,0,0,0,0,0,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,1,1,0,0,0,0,1]
# データをblog_data.npzファイルに保存する
npy.savez('classdata1.npz',X=views,Y=day_of_week,X_min=min(views),X_max=max(views),X_n=len(views))
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('classdata1.npz')
print(sample_data['X'])
print(sample_data['X_min'])出力結果
[ 95 130 201 165 185 179 153 121 119 223 152 239 198 205 116 100 206 238
242 266 183 122 124 201 203 248 223 207 123]
95
出力はデータが確実にセットされてることを確かめるためにやっているのでやらなくても大丈夫です。
問題設定
データセットを元に分布を表示します。
・例
# データサンプルの分類
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
# データ分布表示関数
def show_data(x,t):
K = npy.max(t) + 1
for k in range(K):
# データ分布の設定
plt.plot(x[t == k], t[t == k], X_col[k],alpha=0.5, linestyle='none',marker='o')
plt.grid(True)
plt.ylim(-.5, 1.5)
plt.xlim(X_min, X_max)
plt.yticks([0,1])
# データ生成
# データセットの取り出し
sample_data = npy.load('classdata1.npz')
X_min = sample_data['X_min']
X_max = sample_data['X_max']
X_n = sample_data['X_n']
X = sample_data['X']
X_col = ['cornflowerblue','gray']
# 目標データ
T = sample_data['Y']
print('X=' + str(npy.round(X,2)))
print('T=' + str(T))
flg = plt.figure(figsize=(3,3))
show_data(X,T)
plt.show()・出力結果
X=[ 95 130 201 165 185 179 153 121 119 223 152 239 198 205 116 100 206 238
242 266 183 122 124 201 203 248 223 207 123]
T=[1 1 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 0 1]
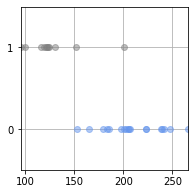
今回は一次元の入力を2クラスに分類する問題となるので一つ基準となるラインを決めれば解決できそうです。
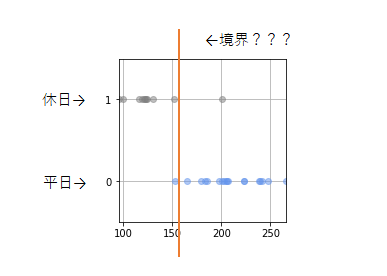
実際のところのこの問題もその境界となる値を決めることになります。
このときの境界を「決定境界」と言います。まずはこの決定境界を導出することが目標となります。
※この記事では導出するとこまではいけませんでした。
確率表現と最尤推定
先にカンニングした感じだとしばらくPythonによる実装はでてこないです。
実装重視の場合は飛ばしてもOK。
そしてロジスティック関数がでてきた辺りから数学的な理解が結構難解になっていく印象です。
確率表現
1次元入力による単純なクラス分類であっても、データを2分割するための直線を引いた場合に確実にクラスを分け切ることができません。
先ほどの出力結果を見直してみます。
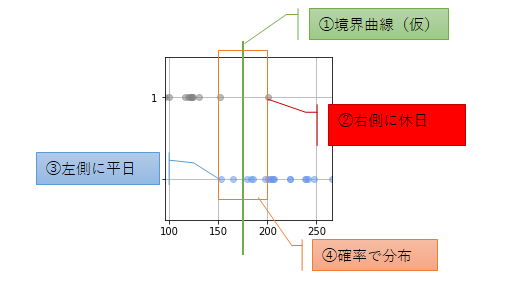
①:まずはそれらしい決定境界を引きます。
ざっくり言えば、その直線の左側が休日クラス、右側が平日クラスと分類できます。
②、③:しかし当然ながら単純に値で完全に二分することはできず、値だけでみると誤判定されるものが出てきます。
④:この部分の領域については、平日と休日のどちらも存在することになります。
どちらのクラスも存在しうる領域にどちらのクラスがどの程度存在するかを確率による表現するわけです。
今回のデータセットにおいてデータを仮に、必ず休日に分類されるデータA、休日と平日が混合するデータB、必ず平日に分類されるデータCに分類します。
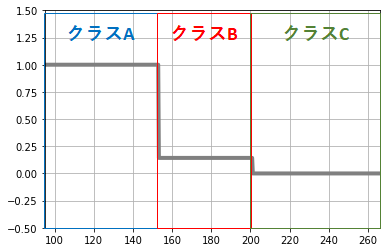
このように分類した場合、各クラスの値がそのまま休日である確率と言うことができます。
つまりアクセス数「x」が休日である確率は特定の範囲で以下のように表現できます。
クラスA:x < 153 ⇒ 1
クラスB:153 ≦ x ≦ 201 ⇒ 0.125
クラスC: 201 < x ⇒ 0
このように、xに対する休日で確率は条件付き確率を使って以下のように表現します。
※確率的な表現を行う上で少し重要と思われる。

グラフはPythonで実装しましたがダサい実装になったのと本筋には関係ないので無視してよいです。
# 確率での表現
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
def func(xline,b_B,b_C,class_B_value):
yline=[]
for i in xline:
if i < b_B:
yline.append(1)
elif i < b_C:
yline.append(class_B_value)
else:
yline.append(0)
return yline
# データ生成
# データセットの取り出し
sample_data = npy.load('classdata1.npz')
X_min = sample_data['X_min']
X_max = sample_data['X_max']
X_n = sample_data['X_n']
X = sample_data['X']
X_col = ['cornflowerblue','gray']
# 目標データ
T = sample_data['Y']
# 平日リスト
w_days = npy.zeros(npy.count_nonzero(T == 0))
w_num = 0
# 休日リスト
h_days = npy.zeros(npy.count_nonzero(T != 0))
h_num = 0
# 平日データと休日データの分割
for i in range(X_n):
if T[i] == 0:
w_days[w_num] = X[i]
w_num = w_num + 1
else:
h_days[h_num] = X[i]
h_num = h_num + 1
# クラス範囲の設定
border_B = min(w_days)
border_C = max(h_days)
class_A = []
class_B = []
class_C = []
class_B_count = []
print(border_B)
print(border_C)
for num in w_days:
# 平日はクラスBかCに割り振る
if num < border_C:
class_B.append(num)
class_B_count.append(0)
else:
class_C.append(num)
for num in h_days:
# 休日はクラスAかBに割り振る
if num < border_B:
class_A.append(num)
else:
class_B.append(num)
class_B_count.append(1)
xline = npy.linspace(X_min, X_max, 500)
b_value = npy.mean(class_B_count)
yline = func(xline, border_B, border_C, b_value)
print(npy.round(b_value,3))
plt.grid(True)
plt.xlim(X_min, X_max)
plt.ylim(-.5, 1.5)
plt.plot(xline,yline,color='gray',linewidth=4)
最尤推定
ここからは最尤推定という考え方を扱っていきます。
機械学習における分類の仕組みを理解しようとする上では避けては通れないものです(多分)。
最尤推定とは統計的な推定手法の一つで、「最も尤もらしい値を推定する」ことになります。
ここで上記の例を以下のモデルで考えてみます。

「w」はt=1、クラスBが休日である確率を表しているので、とりうる範囲は0から1までとなります。
上記の例ではクラスBのデータは[0、0、0、0、0、0、0、1]となっているのでこれを事象Tとして考えていきます。
このとき、事象Tを生成する最も妥当なwの値を考えることが最尤推定になるそうです。
また、事象Tがモデルにより生成される確率のことを尤度と言います。
ちなみに結果は分かり切っています。0.125(1/8)です。
答えが分かっていると逆になにをしているのか理解しにくいかもしれません。
手始めにw=0.1のモデルを考えていきます。
w=0.1というのはクラスBの範囲のデータが休日(1)である確率が「0.1」である場合になるので、尤度は以下のように算出することができます。
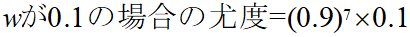
この場合の尤度は約「0.0478」となります。
最尤推定は0から1の範囲でこの尤度が最大になる点を求めることになります。
さて、0から1の範囲で調べていくことになりますが、手動で一つ一つ調べていくのは現実不可能なのでこれまでの考えを一般化します。
一般化すると以下の式で考えることができます。
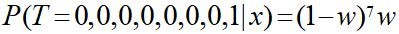
無理にpythonで実装する必要はありませんがpythonで実装し走査すると以下のような結果が得られます。
・実装例
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
def function(w):
return (1-w)**7*w
W = npy.linspace(0, 1, 400)
Y = function(W)
plt.grid(True)
plt.xlim(0, 1)
plt.ylim(-.01, 0.06)
plt.plot(W,Y,color='gray',linewidth=4)
max_w = W[npy.argmax(Y)]
max_y = max(Y)
print(npy.round(max_w,3))
print(npy.round(max_y,3))・出力結果
0.125
0.049

最大の尤度は「0.049」でそのときのwは「0.125」と求めることができました。
数学的に考える最尤推定
最尤推定を行う際の尤度を求める関数を尤度関数(L(θ))と言います。
※likelihoodのL
※θは上記のwに相当
このとき最尤数底は尤度関数(L(θ))が最大になる場合を求める、つまりは尤度関数を微分し0になるときを求めることになります。

ここで冷静に考えてみると今回のデータ例だと尤度関数は以下のようになります。

今回の例ではθの8次元の式になることが分かり、今回はデータが8つと決まっていますがデータ数が増えると微分して解を求めるための計算はかなり大変になってきます。
そのため、次元を下げるために対数をとることが一般的であるようです。
尤度関数の対数をとった関数を対数尤度関数と言います。
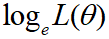
両辺の対数を取った場合、対数尤度関数を最大にするθはそのまま尤度関数を最大にするθとなります。
つまり、最尤推定は対数尤度関数を微分したときに0になるθを求めることとなります。

だいたいここまでOKだと思います。
辛いですが、復習がてら今回の例で解いてみます。
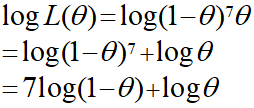

しっかりと0.125が求められました。
うーん、これはすっきり。
今回は最尤推定の考え方まで。
・今回のソース
python_dev/Classification1.ipynb at master · wantanblog/python_dev · GitHub