分類の続き。
2次元入力2クラスの分類の問題設定
前回までの記事では簡単な1次元入力の分類を行いました。
今回は入力要素を2次元にして考えてみます。
↓↓前回の記事
問題提起
前回は、アクセス数(ページビュー数)という1次元の入力に対して、その日が平日か、休日かを分類するという問題について考えてみました。
今回は入力要素を2つにして同様の事象を考えていきたいと思います。
今回は入力要素を「アクセス数(ページビュー数)」と「1ユーザ当たりのページビュー数(以下、UP値)」としていきます。
お馴染みグーグルアナリティクスから、とある月の一日当たりのアクセス数とユーザ数を取得して、アクセス数はそのまま使い、ユーザ数とアクセス数からユーザ当たりのアクセス数を算出します。
その二つの入力値から前回と同じく、平日か休日かを分類するということを行っていきます。
最終的には2次元入力における決定境界を設定することを目標とします。
以下ではPythonでデータ準備を行います。
・データ準備例
# データセット準備
import numpy as npy
# データ生成
views =[95,130,201,165,185,179,153,121,119,223,152,239,198,205,116,100,206,238,242,266,183,122,124,201,203,248,223,207,123]
users =[56,67,154,138,147,133,118,63,73,155,94,191,156,136,83,72,149,163,156,157,140,74,89,103,155,196,157,130,82]
# 1=休日、0=平日
day_of_week=[1,1,0,0,0,0,0,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,1,1,0,0,0,0,1]
N=len(views)
T2 = npy.zeros((N,2), dtype=npy.uint8)
X=npy.zeros((N,2))
uvlist=npy.zeros(N)
#データの設定
for i in range(N):
# 1ユーザ当たりのページビュー数
uperv=round(views[i]/users[i],3)
uvlist[i]=uperv
# データの設定(ビュー数、ユーザあたりのページビュー数)
X[i]=[views[i],uperv]
# 休日[0,1] 平日[1,0]
if day_of_week[i] == 1:
T2[i]=[0,1]
else:
T2[i]=[1,0]
X_range0=[min(views)*0.9,max(views)*1.1]
X_range1=[min(uvlist)*0.9,max(uvlist)*1.1]
# データをclassdata2.npzファイルに保存する
npy.savez('classdata2.npz',X=X,T2=T2,X_range0=X_range0,X_range1=X_range1,X_n=N)データの生成は今回は手作りです。
平日と休日の表現に関しては今後の実装の関係で以下のような表現を行っています。
・ T2(平日、休日を表すクラス分類)
・休日⇒[0,1]
・平日⇒[1,0]
また、グラフの表示範囲を以下のように設定しています。
・X_range0
アクセス数のグラフ上の表示範囲。
最小値の0.9倍から開始し、最大値の1.1倍まで表示する。
・X_range1
UP値のグラフ上の表示範囲。
最小値の0.9倍から開始し、最大値の1.1倍まで表示する。
データの設定(PG上)
上記で設定したデータファイルからデータを取得して、今後のプログラム上で使用するために変数に設定しておきます。
# データの設定
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('classdata2.npz')
# 入力値の設定
X=sample_data['X']
# クラス(答え)の設定
T2=sample_data['T2']
# アクセス数の表示範囲設定
X_range0=sample_data['X_range0']
# UP値の表示範囲設定
X_range1=sample_data['X_range1']
# データ数の設定
N=sample_data['X_n']プログラムで使用するだけなのでこれだけ。
データの散布表示
続いて設定したデータをPythonによって散布表示してみます。
・実装例
import matplotlib.pyplot as plt
%matplotlib inline
# データ表示
def show_data2(x,t):
wk,K = t.shape
c=[[.5,.5,.5],[1,1,1]]
for k in range(K):
# 平日はグレー表示、休日は白抜き表示
plt.plot(x[t[:, k]==1,0],x[t[:, k]==1,1],linestyle='none',markeredgecolor='black',marker='o',color=c[k],alpha=0.8)
plt.grid(True)
plt.figure(figsize=(5,3))
plt.subplots_adjust(wspace=0.5)
show_data2(X, T2)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.show()
平日のデータ(クラスA)をグレー、休日のデータ(クラスB)を白抜きとしてデータをプロットしています。
抽出したデータがよかったのかかなりきっぱりと別れていて、明確な線が引けそうですね。
ロジスティック回帰モデル
3D曲線モデルの描画
1次元入力のモデルの際にも活用したロジスティック回帰モデルを使用します。
入力値のアクセス数とUP値をXとして、休日である確率を以下のように表現します。
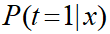
ここで、入力パラメータを3つにしたモデルを立てます。

このモデルをロジスティック関数(ガウス関数)に適用します。

このロジスティック関数に今回のデータを適用して3D曲面モデルをPythonで実装します。
・実装例
# 3D曲面の描画
from mpl_toolkits.mplot3d import axes3d
# ロジスティック回帰モデル
def logistic2(x0,x1,w):
y=1/(1+npy.exp(-(w[0]*x0+w[1]*x1+w[2])))
return y
# 3D曲面の描画
def show3d_logistic2(ax, w):
xn=50
x0=npy.linspace(X_range0[0],X_range0[1],xn)
x1=npy.linspace(X_range1[0],X_range1[1],xn)
xx0,xx1 = npy.meshgrid(x0,x1)
y=logistic2(xx0,xx1,w)
ax.plot_surface(xx0,xx1,y,color='blue',edgecolor='gray',rstride=5,cstride=5,alpha=0.3)
# 3Dにデータをプロット
def show_data2_3d(ax,x,t):
c = [[.5,.5,.5],[1,1,1]]
for i in range(2):
ax.plot(x[t[:,i] == 1,0],x[t[:,i] == 1,1],i,marker='o',color=c[i],markeredgecolor='black',linestyle='none',markersize=5,alpha=0.8)
ax.view_init(elev=25,azim=-30)
Ax=plt.subplot(1,1,1,projection='3d')
W=[-0.0155,2.1,-0.01]
show3d_logistic2(Ax,W)
show_data2_3d(Ax,X,T2)
plt.show()・出力結果

モデルを描写するためにはパラメータWを決める必要があります。
ここは入力データによって設定する必要があるので、表示をしながら徐々に設定を行い最終的に以下を設定しました。
W=[-0.0155,2.1,-0.01]
縦軸は休日である確率を表しています。
等高線による図示
次にお馴染みですが、3D曲線モデルを等高線で図示してみます。
1次元入力でも同じようなことをやりましたが、特に重要になるのは決定境界となる「0.5」の部分です。
但し、今回は入力パラメータをよさそうな感じに適当に決めているので、今回の問題に対する決定境界はのちほど確定させます。
・実装例
# 等高線表示
def show_contour_logistic2(w):
xn = 30
x0=npy.linspace(X_range0[0],X_range0[1],xn)
x1=npy.linspace(X_range1[0],X_range1[1],xn)
xx0,xx1 = npy.meshgrid(x0,x1)
y=logistic2(xx0,xx1,w)
cont=plt.contour(xx0,xx1,y,levels=(0.3,0.5,0.7),colors=['k','cornflowerblue','k'])
cont.clabel(fmt='%.1f',fontsize=10)
plt.grid(True)
plt.figure(figsize=(5,3))
W=[-0.0155,2.1,-0.01]
show_contour_logistic2(W)
plt.show()・出力結果

交差エントロピー誤差
前回1次元入力のデータセットでも活用した交差エントロピー誤差を2次元入力にも適用します。
・交差エントロピー誤差

今回も最小値を求めるので、この式をパラメータW(w0、w1、w2)ごとに偏微分を行います。
計算方法は前回の記事と同様なので省略しますが、偏微分の結果は以下のようになります。
・交差エントロピー誤差の偏微分
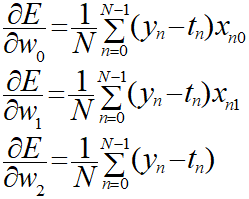
これらの式をPythonにより実装します。
・実装例
from scipy.optimize import minimize
# 交差エントロピー誤差
def cee_logistic2(w,x,t):
X_n=x.shape[0]
y=logistic2(x[:,0],x[:,1],w)
cee = 0
for n in range(len(y)):
cee = cee -(t[n,0]*npy.log(y[n])+(1-t[n,0])*npy.log(1-y[n]))
cee = cee/X_n
return cee
# 交差エントロピー誤差の微分
def dcee_logistic2(w,x,t):
X_n=x.shape[0]
y=logistic2(x[:,0],x[:,1],w)
dcee = npy.zeros(3)
for n in range(len(y)):
dcee[0]=dcee[0]+(y[n]-t[n,0])*x[n,0]
dcee[1]=dcee[1]+(y[n]-t[n,0])*x[n,1]
dcee[2]=dcee[2]+(y[n]-t[n,0])
dcee = dcee/X_n
return dcee
# ロジスティック回帰モデルのパラメータサーチ
def fit_logistic2(w_init,x,t):
res=minimize(cee_logistic2,w_init,args=(x,t),jac=dcee_logistic2,method="CG")
return res.x
plt.figure(1,figsize=(10,3))
plt.subplots_adjust(wspace=0.5)
Ax=plt.subplot(1,2,1,projection='3d')
W_init =[-0.10,1,-0.01]
W =fit_logistic2(W_init,X,T2)
print("w0={0:.2f},w1={1:2f},w2={2:2f}".format(W[0],W[1],W[2]))
show3d_logistic2(Ax,W)
show_data2_3d(Ax,X,T2)
cee = cee_logistic2(W,X,T2)
print("CEE={0:2f}".format(cee))
Ax=plt.subplot(1,2,2)
show_data2(X,T2)
show_contour_logistic2(W)
plt.show()・出力結果
w0=-0.01,w1=1.000602,w2=-0.009564
CEE=0.975249

パラメータの導出にはscipy.optinizeのminimize関数を用いています。
今回の決定境界は等高線の「0.5」の線の部分になります。
これにより、決定境界の左側に存在するデータは休日、右側に存在するデータは平日に分類することができます。
アクセス数だけで平日休日を判定するのはかなり雑な感じがしましたが、入力値を二つにすることによって適切な要素を使えばかなり正確に割り振れる気がしますね。
ーーーーーーーーーーーーーーー
・今回のソース
python_dev/Classification_2-1.ipynb at master · wantanblog/python_dev · GitHub