前回までの流れ
2層ニューラルネットワークモデルの実装の続きです。
前回はニューラルネットワークモデルの本体を実装しましたが、それだけでは重みを適切に設定することができないので、有効活用ができていませんでした。
なので、今回は重み設定して、実装したニューラルネットワークモデルを問題解決に活用できるようにすることが目標となります。
・前回の記事
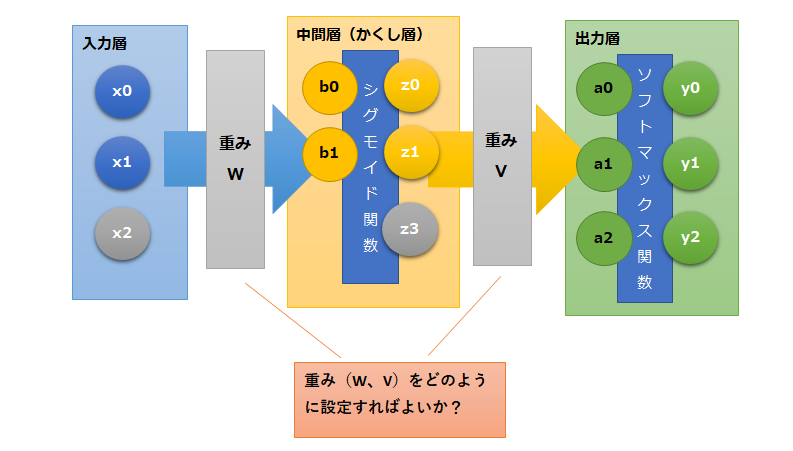
ニューラルネットワークの適切な重みを設定するには
平均交差エントロピー誤差
今回の問題はそもそも分類の問題であり、適切なパラメータを設定するためには平均交差エントロピー誤差が最小になる重みを求めるという方針で考えていきます。
なので、まずは平均交差エントロピー誤差を実装しておきます。

・実装例
# 平均交差エントロピー誤差
def CE_FNN(wv,M,K,x,t):
N,D = x.shape
y,a,z,b=FNN(wv,M,K,x)
ce = -npy.dot(t.reshape(-1),npy.log(y.reshape(-1))) / N
return ce
数値微分の導入
勾配法を適用するために誤差関数の偏微分が必要になります。
今回は適切な重みを求めるために数値微分(法)を用います。
■数値微分(法)
当該関数において微分を行い導関数を求めることが困難な場合などに近似による微分計算を行う手法のことです。
具体的に考えてみます。
平均交差エントロピー誤差のグラフを例示します。
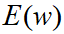
勾配法における偏微分ではある地点(w*)の傾き「∂E/∂w」を求めます。
求めた「∂E/∂w」に学習率をかけて、w*からその分だけ位置をずらしていき極小値となる底に近づけていくのでした。

数値微分では偏微分を行わずに傾きを近似的に求めます。
求め方は、ある地点(w*)からεだけずらした地点間を結び傾きを求めることにより近似値とします。

数式では以下のように表現することができます。

一般的にはεの値が小さいほど、求めたい地点(w*)に近づくため精度が上がります。
実際にパラメータをいじってみた感じだとεの値が大きいと発散する可能性があり、小さすぎると極小値にたどり着かない可能性もあります。
今回の問題の場合は三次元なので以下のように行う必要があります。
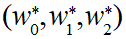
重みパラメータの各wについて偏微分を行う必要があるので、実際には以下のように行います。

数値微分の実装
上記の数値微分をPythonで実装してみます。
・実装例
# 数値微分式
def dCE_FNN_num(wv,M,K,x,t):
epsilon = 0.001
dwv = npy.zeros_like(wv)
# 重みごとにループ
for iwv in range(len(wv)):
wv_modified = wv.copy()
# E(w* -ε)
wv_modified[iwv] = wv[iwv]-epsilon
mse1 = CE_FNN(wv_modified,M,K,x,t)
# E(w* +ε)
wv_modified[iwv] = wv[iwv]+epsilon
mse2 = CE_FNN(wv_modified,M,K,x,t)
# ∂E/∂wの近似値
dwv[iwv] = (mse2 - mse1)/(2*epsilon)
return dwv
勾配法の実装
実装した数値微分式を用いて、勾配法の実装を行います。
※1000ステップで実装しているので、そのまま実行すると多少時間がかかる可能性があります。
・実装例
# 勾配法の実装
def Fit_FNN_num(wv_init,M,K,x_train,t_train,x_test,t_test,n,alpha):
# 重みの初期値
wv = wv_init
err_train =npy.zeros(n)
err_test = npy.zeros(n)
wv_hist = npy.zeros((n,len(wv_init)))
for i in range(n):
# 重みを遷移させる
wv = wv -alpha*dCE_FNN_num(wv,M,K,x_train,t_train)
# 訓練データの誤差
err_train[i] = CE_FNN(wv,M,K,x_train,t_train)
# テストデータの誤差
err_test[i] = CE_FNN(wv,M,K,x_test,t_test)
# 重みの遷移
wv_hist[i,:]=wv
return wv, wv_hist, err_train, err_test
M = 2
K = 3
# 重みの初期値設定
npy.random.seed(1)
WV_init = npy.random.normal(0,0.01,M*3+K*(M+1))
# ステップ数の設定
N_step=1000
# 学習率の設定
alpha=0.215
# 勾配法
WV,WV_hist,Err_train,Err_test=Fit_FNN_num(WV_init,M,K,X_train,T_train,X_test,T_test,N_step,alpha)
# 誤差の表示
plt.figure(1,figsize=(3,3))
plt.plot(Err_train, 'black',label='training')
plt.plot(Err_test,'blue',label='test')
plt.legend()
plt.show()
plt.figure(1,figsize=(3,3))
plt.plot(WV_hist[:,:M*3], 'black')
plt.plot(WV_hist[:,M*3:],'orange')
plt.show()
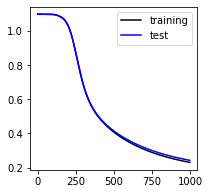
print(WV)【出力結果】
・平均交差エントロピー誤差の遷移
・重みの遷移

黒はW、オレンジはVの最適化された重みの値を表しています。
500ステップぐらいまで誤差が大分小さくなっていることが分かり、1000ステップ付近では収束してきていることが分かります。
重みについても1000ステップ付近ではグラフがなだらかになってきていますが、まだ傾きがあるので、このまま続けていくと多少値が変わっていく可能性があります。
・重みの出力値
[ 0.80239664 -4.37401759 1.63008767 -0.43057265 4.0529699 -1.04155072
4.44972948 -4.77215962 -0.22252789 0.82773738 1.22970944 0.00674128
-5.26573695 3.54561771 0.20971004]
Fit_FNN_numから出力されるWVは最終的な重みの値となるので、上記の出力値が1000ステップ後の重みの値となり今回の最終的な最適化された重みとなります。
ニューラルネットワークモデルによる分類
上記で実装したニューラルネットワークモデルと、最適な重みを使用してテストデータの分類を行います。
・実装例
# 境界線の表示
def show_FNN(wv,M,K):
# グラフを60×60に分割
xn = 60
x0 = npy.linspace(X_range0[0],X_range0[1],xn)
x1 = npy.linspace(X_range1[0],X_range1[1],xn)
xx0, xx1 = npy.meshgrid(x0,x1)
x = npy.c_[npy.reshape(xx0,xn*xn,1),npy.reshape(xx1,xn*xn,1)]
y,a,z,b = FNN(wv,M,K,x)
plt.figure(1,figsize=(4,4))
for ic in range(K):
f = y[:,ic]
f = f.reshape(xn,xn)
f = f.T
# 存在確率が0.5と0.7の部分に等高線をひく
cont = plt.contour(xx0,xx1,f,levels=[0.5,0.7],colors=['blue','black'])
cont.clabel(fmt='%.1f',fontsize=9)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.figure(1,figsize=(3,3))
Show_data(X_test,T_test)
print(WV)
show_FNN(WV,M,K)
plt.show()
・出力結果

訓練データによって算出した境界をテストデータに適用します。
今回はデータの分類がはっきりしているため、直線による分類となっています。
ーーーーーーーー
・今回のソース
python_dev/Neural_net2_prod.ipynb at master · wantanblog/python_dev · GitHub