前回までの
まず最初にMNISTという手書き文字画像データセットに対して、Kerasライブラリを活用してニューラルネットワークを実装して手書き文字の識別を行いました。
その後、正答率の改善のために活性化関数の検討を行い、シグモイド関数からReLu関数へと変更を行いました。
活性化関数ごとの結果を比較すると以下のような結果になりました。
■最終正答率
・シグモイド関数
TEST loss: 0.4908383786678314 TEST accuracy: 0.897599995136261 Computation time:2.425 sec
・ReLU関数
TEST loss: 0.24740302562713623 TEST accuracy: 0.9282000064849854 Computation time:2.326 sec
ニューラルネットワークにおける入力情報
これまでのニューラルネットワークは以下のようなモデルを想定して構築してきました。

今回は特にこの入力層における入力情報に着目してみます。
実際には「28×28」の文字画像を用いてやりましたが、ここでは簡易的に「7×7」を用いて考えていきます。
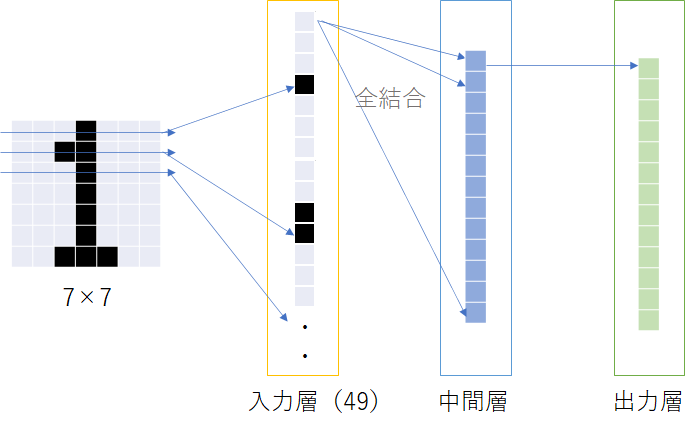
入力情報は「7×7」のセルを持った画像で、これをニューラルネットワークにかける際には1列49個の配列として扱うことになります。
つまりは、二次元情報を一次元情報として扱っています。
これは言い換えると、一次元情報を入れ替えても規則に従って処理を行えば結果は変わらないということであり、また二次元がもつ空間情報が失われているということでもあります。
空間フィルターと畳み込み演算
空間フィルター
二次元の空間情報というのは画像で言うところ直線や曲線などの形を表す情報のことです。
このような情報を処理するための空間フィルターという手法を用いるのが一般的なようです。
ここでは「3×3」のセルを持ったフィルターを使用してみます。

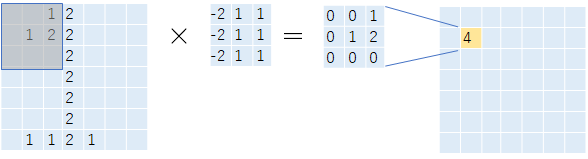
このように「3×3」のフィルターを元画像に適用していき、フィルターとの積を合算して数値を算出していきます。
これを画像の全領域に対してかけていくことによって、最終的な結果を求めます。
サンプルの例ではフィルターをかけていくことによって、以下のような出力結果を得ることができます。
これにより一定の空間を圧縮変換していることから、二次元の空間情報を活用しているイメージができると思います。
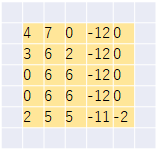
このようにフィルターをかけていく処理を畳み込み演算と言います。
機械学習について勉強する前にも聞く機会があった畳み込みというのはこのようなことを表していたのですね。
パディング
前回の図からも様子が分かりますが、一般的にフィルターをそのまま適用すると、画像サイズが一回り小さくなります。
フィルターは幾層に連なって使用することがあるため、元々の画像が縮小されてしまうことになります。
この対応策としてパディングという手法が使われることがあります。
パディングでは元々のセルの周りを囲うように「0」のダミーセルを設定していきます。
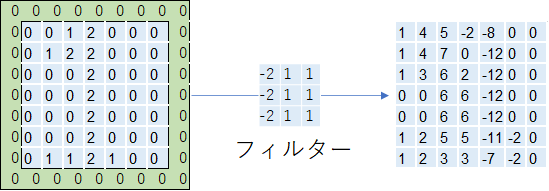
これによりフィルターを通しても元々の画像サイズと買わない出力結果を取得することができるようになります。
フィルターの実装
ここからは上記のフィルターをPythonで実装します。
なのでここからはMNISTの画像データを扱うので28×28の画像を扱います。
データ準備
処理を行うための下準備で、前回の記事までの再掲です。
# インポートセット from keras.datasets import mnist import numpy as npy from keras.utils import np_utils import matplotlib.pyplot as plt %matplotlib inline
# データの読み出し mnist_raw_data = npy.load('mnist_raw.npz') x_train=mnist_raw_data['x_train'] y_train=mnist_raw_data['y_train'] x_test=mnist_raw_data['x_test'] y_test=mnist_raw_data['y_test']
#データ整形 from keras.utils import np_utils # 28×28のまま扱う x_train=x_train.reshape(60000,28,28,1) # 0-255⇒0-1に変換 x_train=x_train.astype('float32') x_train=x_train/255 # 1-of-K符号化法で表現 num_classes=10 y_train=np_utils.to_categorical(y_train,num_classes) x_test=x_test.reshape(10000,28,28,1) x_test=x_test.astype('float32') x_test=x_test/255 y_test=np_utils.to_categorical(y_test,num_classes)
フィルター処理の実装
次に本題のフィルターを実装していきます。
今回は一番目の画像に対してフィルターをかけ、出力例を示します。
・実装例
import matplotlib.pyplot as plt %matplotlib inline id_img = 0 # フィルター1の実装 myfil1 = npy.array([[1,1,1],[1,1,1],[-2,-2,-2]],dtype=float) # フィルター2の実装 myfil2 = npy.array([[-2,1,1],[-2,1,1],[-2,1,1]],dtype=float) x_img = x_train[id_img,:,:,0] img_h = 28 img_w = 28 x_img = x_img.reshape(img_h,img_w) out_img1 = npy.zeros_like(x_img) out_img2 = npy.zeros_like(x_img) #フィルタ処理 for ih in range(img_h -3 +1): for iw in range(img_w -3 +1): # 元画像を3×3の領域に切り取る img_part = x_img[ih:ih + 3, iw:iw + 3] # フィルタ1の処理 out_img1[ih + 1, iw + 1] = npy.dot(img_part.reshape(-1),myfil1.reshape(-1)) # フィルタ2の処理 out_img2[ih + 1, iw + 1] = npy.dot(img_part.reshape(-1),myfil2.reshape(-1)) # 表示 plt.figure(1,figsize=(12,3.2)) plt.subplots_adjust(wspace=0.5) plt.gray() plt.subplot(1,3,1) plt.pcolor(1-x_img) plt.xlim(-1,29) plt.ylim(29,-1) plt.subplot(1,3,2) plt.pcolor(-out_img1) plt.xlim(-1,29) plt.ylim(29,-1) plt.subplot(1,3,3) plt.pcolor(-out_img2) plt.xlim(-1,29) plt.ylim(29,-1) plt.show()
・出力結果
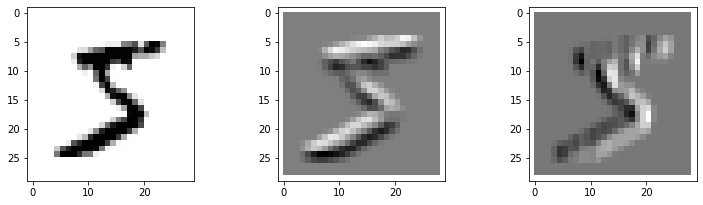
・フィルター1
縦のエッジを強調する。
・フィルター2
横のエッジを強調する。
フィルターに関しては設定する数値に工夫をすることによって、縦横以外にも斜めの強調や画像の平滑化など、必要な特長に応じたフィルターを設定することができます。
また、フィルターは全合計が「0」になるように設計を行うことで、0を検知レベルの基準とすることができるので結果を分析するときに分かりやすいと言われています。
畳み込みニューラルネットワーク(CNN)の実装
次に、これまで実装したニューラルネットワークにフィルターを追加し、畳み込みニューラルネットワークの実装を行うことにします。
これまで通り、Kerasを用いた実装になります。
Kerasを用いてモデルを構築すると、フィルター自体にも学習により最適化されていくことになります。
・実装例
# CNNモデルの実装 npy.random.seed from keras.models import Sequential from keras.layers import Conv2D, MaxPooling2D from keras.layers import Activation, Dropout, Flatten, Dense from keras.optimizers import Adam import time model = Sequential() model.add(Conv2D(8,(3,3),padding='same', input_shape=(28,28,1),activation='relu')) model.add(Flatten()) model.add(Dense(10, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer=Adam(),metrics=['accuracy']) startTime = time.time() history = model.fit(x_train,y_train,batch_size=1000, epochs=20,verbose=1,validation_data=(x_test,y_test)) score = model.evaluate(x_test,y_test,verbose=0) print('Test loss:', score[0]) print('Test accuracy:', score[1]) print("Computation time:{0:3f}sec".format(time.time() - startTime))
・出力結果
Epoch 1/20 60/60 [==============================] - 3s 48ms/step - loss: 0.8223 - accuracy: 0.8138 - val_loss: 0.3429 - val_accuracy: 0.9063 Epoch 2/20 60/60 [==============================] - 3s 46ms/step - loss: 0.3080 - accuracy: 0.9126 - val_loss: 0.2628 - val_accuracy: 0.9245 Epoch 3/20 60/60 [==============================] - 3s 46ms/step - loss: 0.2472 - accuracy: 0.9304 - val_loss: 0.2256 - val_accuracy: 0.9365 Epoch 4/20 60/60 [==============================] - 3s 46ms/step - loss: 0.2084 - accuracy: 0.9420 - val_loss: 0.1895 - val_accuracy: 0.9470 Epoch 5/20 60/60 [==============================] - 3s 46ms/step - loss: 0.1782 - accuracy: 0.9507 - val_loss: 0.1639 - val_accuracy: 0.9560 Epoch 6/20 60/60 [==============================] - 3s 46ms/step - loss: 0.1543 - accuracy: 0.9576 - val_loss: 0.1469 - val_accuracy: 0.9603 Epoch 7/20 60/60 [==============================] - 3s 50ms/step - loss: 0.1363 - accuracy: 0.9633 - val_loss: 0.1321 - val_accuracy: 0.9634 Epoch 8/20 60/60 [==============================] - 3s 52ms/step - loss: 0.1215 - accuracy: 0.9676 - val_loss: 0.1220 - val_accuracy: 0.9644 Epoch 9/20 60/60 [==============================] - 3s 51ms/step - loss: 0.1111 - accuracy: 0.9706 - val_loss: 0.1116 - val_accuracy: 0.9676 Epoch 10/20 60/60 [==============================] - 3s 52ms/step - loss: 0.1018 - accuracy: 0.9730 - val_loss: 0.1080 - val_accuracy: 0.9691 Epoch 11/20 60/60 [==============================] - 3s 52ms/step - loss: 0.0951 - accuracy: 0.9746 - val_loss: 0.1008 - val_accuracy: 0.9712 Epoch 12/20 60/60 [==============================] - 3s 52ms/step - loss: 0.0891 - accuracy: 0.9763 - val_loss: 0.0948 - val_accuracy: 0.9717 Epoch 13/20 60/60 [==============================] - 3s 53ms/step - loss: 0.0838 - accuracy: 0.9770 - val_loss: 0.0897 - val_accuracy: 0.9737 Epoch 14/20 60/60 [==============================] - 3s 53ms/step - loss: 0.0790 - accuracy: 0.9788 - val_loss: 0.0893 - val_accuracy: 0.9735 Epoch 15/20 60/60 [==============================] - 3s 53ms/step - loss: 0.0748 - accuracy: 0.9796 - val_loss: 0.0856 - val_accuracy: 0.9745 Epoch 16/20 60/60 [==============================] - 3s 53ms/step - loss: 0.0724 - accuracy: 0.9802 - val_loss: 0.0826 - val_accuracy: 0.9759 Epoch 17/20 60/60 [==============================] - 3s 53ms/step - loss: 0.0686 - accuracy: 0.9818 - val_loss: 0.0823 - val_accuracy: 0.9755 Epoch 18/20 60/60 [==============================] - 3s 52ms/step - loss: 0.0653 - accuracy: 0.9824 - val_loss: 0.0805 - val_accuracy: 0.9768 Epoch 19/20 60/60 [==============================] - 3s 51ms/step - loss: 0.0629 - accuracy: 0.9828 - val_loss: 0.0776 - val_accuracy: 0.9770 Epoch 20/20 60/60 [==============================] - 3s 51ms/step - loss: 0.0600 - accuracy: 0.9837 - val_loss: 0.0766 - val_accuracy: 0.9763 Test loss: 0.07661159336566925 Test accuracy: 0.9763000011444092 Computation time:62.010370sec
ここにきて正答率は「0.976」まで向上しました。
エポック数を増すごとに徐々に向上していく様子が分かります。
実装的に今回主に追加したのは以下の行です。
model.add(Conv2D(8,(3,3),padding='same', input_shape=(28,28,1),activation='relu')) model.add(Flatten())
ここでは「3×3」のフィルターを8枚活用し、「padding='same'」で元々の画像とサイズが変わらないようにするパディングを追加しています。
Conv2Dの出力は4次元なので、Dense層の入力値である「バッチ数、フィルター数×出力画像縦幅×出力画像横幅」の2次元情報に変換を行うのが「model.add(Flatten())」の処理になります。
出力結果の確認
出力結果を画像で確認しておきます。
# テストデータの投入 def show_prediction(): n_show = 150 y=model.predict(x_test) plt.figure(2,figsize=(12,8)) plt.gray() for i in range(n_show): plt.subplot(10,15,i+1) x=x_test[i,:] x=x.reshape(28,28) plt.pcolor(1-x) wk=y[i,:] prediction=npy.argmax(wk) plt.text(22,25.5,"%d"% prediction,fontsize=12) if prediction != npy.argmax(y_test[i,:]): plt.plot([0,27],[1,1],color='cornflowerblue',linewidth=5) plt.xlim(0,27) plt.ylim(27,0) plt.xticks([],"") plt.yticks([],"") show_prediction() plt.show()

畳み込み演算を組み込む前と比較して、かなり正答率が向上している様子が分かると思います。
ーーーーーーーーーーーーー
・今回のソース
python_dev/MNIST_3.ipynb at master · wantanblog/python_dev · GitHub