今回は前記事のKerasライブラリを活用して手書き数字の認識に挑戦していきます。
実装部は全てjupyter notebookで実施しています。
MNISTデータベース
MNIST
MNISTは、手書き数字画像60,000枚と、テスト画像10,000枚を集めた、画像データセットです。
今回のようにディープラーニングの入門学習などにもよく用いられるようです。
参考:MNIST handwritten digit database, Yann LeCun, Corinna Cortes and Chris Burges
データの取得
Kerasでは以下のようにデータセットの取得を行うことができます。
学習に使用する訓練データを「x_train」として、学習結果の検証に使うテストデータを「x_test」としています。
# MNISTデータダウンロード from keras.datasets import mnist (x_train, y_train),(x_test, y_test)=mnist.load_data()
・ファイルへのデータの保存
※使用には必須ではない
# データの保存 npy.savez('mnist_raw.npz',x_train=x_train,y_train=y_train,x_test=x_test,y_test=y_test)
・ファイルからデータの取り出し
※使用には必須ではない
# データの読み出し mnist_raw_data = npy.load('mnist_raw.npz') x_train=mnist_raw_data['x_train'] y_train=mnist_raw_data['y_train'] x_test=mnist_raw_data['x_test'] y_test=mnist_raw_data['y_test']
データ構造の確認
学習に活用するライブラリの詳細な中身はまだしも、活用するデータについては確実に抑えておいた方がいいでしょう。
■x_train
学習を行う画像データが以下のような形式で格納されています。
・実装例
print(x_train[0])
・出力結果
[[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 3 18 18 18 126 136 175 26 166 255 247 127 0 0 0 0] [ 0 0 0 0 0 0 0 0 30 36 94 154 170 253 253 253 253 253 225 172 253 242 195 64 0 0 0 0] [ 0 0 0 0 0 0 0 49 238 253 253 253 253 253 253 253 253 251 93 82 82 56 39 0 0 0 0 0] [ 0 0 0 0 0 0 0 18 219 253 253 253 253 253 198 182 247 241 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 80 156 107 253 253 205 11 0 43 154 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 14 1 154 253 90 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 139 253 190 2 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 11 190 253 70 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 35 241 225 160 108 1 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 81 240 253 253 119 25 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 45 186 253 253 150 27 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 16 93 252 253 187 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 249 253 249 64 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 46 130 183 253 253 207 2 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 39 148 229 253 253 253 250 182 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 24 114 221 253 253 253 253 201 78 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 23 66 213 253 253 253 253 198 81 2 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 18 171 219 253 253 253 253 195 80 9 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 55 172 226 253 253 253 253 244 133 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 136 253 253 253 212 135 132 16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
x_trainは配列で一つ一つは画像データとして28×28の要素から成っています。
その中の個別要素は0-255の範囲でモノクロカラーの色の濃さを表しているため出力すると上記のようになります。
画像データでも確かにこのように数値化すればプログラムにより認識できそうという感じはしてきますね。
■y_train
・実装例
print(y_train[0])
・出力結果
5
「y」には画像データの正解を表す数値が格納されています。
■イメージとして出力する
先ほどの配列をイメージとして出力してみます。
・実装例
# データのイメージ出力 import numpy as npy import matplotlib.pyplot as plt %matplotlib inline plt.figure(1,figsize=(4,4)) plt.subplots_adjust(wspace=0.5) plt.gray() plt.subplot(1,1,1) img=x_train[0,:,:] plt.pcolor(255-img) plt.text(24.5,26,"%d"%y_train[0],color='cornflowerblue',fontsize=18) plt.xlim(0,27) plt.ylim(27,0) plt.show()
・出力結果
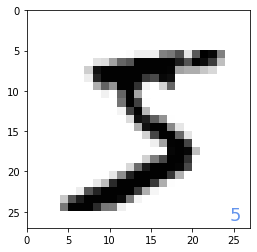
グラフのプロットの色を要素の値から設定することで手書き文字としてのイメージを出力することができました。
2層フィードフォワードネットワークモデルの実装
まずは2層フィードフォワードネットワークモデルにより、手書き数字の認識(分類)問題に挑みます。
データの整形
MNISTから取得したデータをディープラーニングにかけやすくするためにデータ整形を行います。
・実装例
#データ整形 from keras.utils import np_utils # 28×28⇒784配列変換 x_train=x_train.reshape(60000,784) # 0-255⇒0-1に変換 x_train=x_train.astype('float32') x_train=x_train/255 # 1-of-K符号化法で表現 num_classes=10 y_train=np_utils.to_categorical(y_train,num_classes) x_test=x_test.reshape(10000,784) x_test=x_test.astype('float32') x_test=x_test/255 y_test=np_utils.to_categorical(y_test,num_classes) print(x_train[0,150:200]) print(y_train[0])
・出力結果
[0. 0. 0.01176471 0.07058824 0.07058824 0.07058824 0.49411765 0.53333336 0.6862745 0.10196079 0.6509804 1. 0.96862745 0.49803922 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.11764706 0.14117648 0.36862746 0.6039216 0.6666667 0.99215686 0.99215686 0.99215686 0.99215686 0.99215686 0.88235295 0.6745098 0.99215686 0.9490196 0.7647059 0.2509804 0. 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
Kerasライブラリを使用できるように、コメントに記載した内容の通りにデータ整形を行っています。
ニューラルネットワークモデルの定義
簡単な使用方法は前回の記事にも記載しているので、同様に使っていきます。
ネットワークモデルのタイプ
Sequential
中間層
ノードタイプ:Dense
ノード数:16ノード
入力次元:784
活性化関数:シグモイド関数
出力層
ノードタイプ:Dense
ノード数:10ノード
活性化関数:ソフトマックス関数
目的関数
クロスエントロピー誤差
オプティマイザ
Adam
# ニューラルネットワークモデルの定義 from keras.models import Sequential from keras.layers import Dense, Activation from keras.optimizers import Adam npy.random.seed model=Sequential() model.add(Dense(16,input_dim=784,activation='sigmoid')) model.add(Dense(10,activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer=Adam(),metrics=['accuracy'])
学習の実行
上記のネットワークモデルを使用して、データを元に学習を行います。
batch_size=1000、epochs=10としているので、全データを1000個ごとに分割してパラメータ更新を行う。これを10回繰り返す。
・実装例
# 学習の実行 import time start_time=time.time() history=model.fit(x_train,y_train,epochs=10,batch_size=1000,verbose=1,validation_data=(x_test,y_test)) score=model.evaluate(x_test,y_test,verbose=0) print('TEST loss:', score[0]) print('TEST accuracy:', score[1]) print("Computation time:{0:.3f} sec".format(time.time()-start_time))
・出力結果
Epoch 1/10 60/60 [==============================] - 0s 5ms/step - loss: 2.0619 - accuracy: 0.3990 - val_loss: 1.7701 - val_accuracy: 0.5962 Epoch 2/10 60/60 [==============================] - 0s 3ms/step - loss: 1.5951 - accuracy: 0.6823 - val_loss: 1.4248 - val_accuracy: 0.7480 Epoch 3/10 60/60 [==============================] - 0s 3ms/step - loss: 1.3059 - accuracy: 0.7682 - val_loss: 1.1791 - val_accuracy: 0.7974 Epoch 4/10 60/60 [==============================] - 0s 3ms/step - loss: 1.0928 - accuracy: 0.8054 - val_loss: 0.9965 - val_accuracy: 0.8330 Epoch 5/10 60/60 [==============================] - 0s 3ms/step - loss: 0.9339 - accuracy: 0.8368 - val_loss: 0.8598 - val_accuracy: 0.8535 Epoch 6/10 60/60 [==============================] - 0s 3ms/step - loss: 0.8132 - accuracy: 0.8555 - val_loss: 0.7541 - val_accuracy: 0.8699 Epoch 7/10 60/60 [==============================] - 0s 3ms/step - loss: 0.7196 - accuracy: 0.8677 - val_loss: 0.6721 - val_accuracy: 0.8782 Epoch 8/10 60/60 [==============================] - 0s 3ms/step - loss: 0.6458 - accuracy: 0.8769 - val_loss: 0.6062 - val_accuracy: 0.8858 Epoch 9/10 60/60 [==============================] - 0s 3ms/step - loss: 0.5870 - accuracy: 0.8839 - val_loss: 0.5539 - val_accuracy: 0.8904 Epoch 10/10 60/60 [==============================] - 0s 3ms/step - loss: 0.5397 - accuracy: 0.8890 - val_loss: 0.5122 - val_accuracy: 0.8944 TEST loss: 0.512151837348938 TEST accuracy: 0.8944000005722046 Computation time:2.399 sec
パラメータの更新を600回行い、交差エントロピー誤差は「0.512」テストデータによる検証では「0.894」の正答率を出せたことがわかります。
経過の表示
「学習の実行」を行った時点でおおむね目的は果たせていますが、最後に交差エントロピー誤差と正答率の経過をグラフ上に表示していきたいと思います。
・実装例
# 経過表示 plt.figure(1,figsize=(10,4)) plt.subplots_adjust(wspace=0.5) # 交差エントロピー誤差の経過表示 plt.subplot(1,2,1) plt.plot(history.history['loss'],label='trainig',color='black') plt.plot(history.history['val_loss'],label='test',color='cornflowerblue') plt.ylim(0,10) plt.legend() plt.grid() plt.xlabel('epoch') plt.ylabel('loss') # 正答率の経過表示 plt.subplot(1,2,2) plt.plot(history.history['accuracy'],label='training',color='black') plt.plot(history.history['val_accuracy'],label='test',color='cornflowerblue') plt.ylim(0,1) plt.legend() plt.grid() plt.xlabel('epoch') plt.ylabel('accuracy') plt.show()
・出力結果
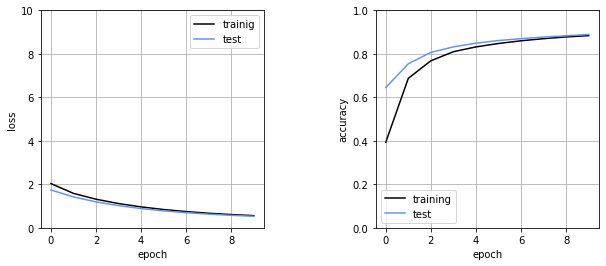
今回の結果では手書き数字という単純な分類でありながら正答率は「0.894」とそこまで高い結果を出すことができませんでした。
今回はまず実装を行うことを重きに置いていたため、次回以降は精度をあげるための工夫を取り入れていきたいと思います。
ーーーーーーーーーーーーー
・今回のソース
python_dev/MNIST_1.ipynb at master · wantanblog/python_dev · GitHub