前回の続き。
オーバーフィッティング(過学習)
パラメータMの設定
前回取り扱った線形基底関数モデルでは、ガウス関数を基底関数として選択し検討を行いました。
その際にパラメータとしてM=4を設定しましたが、このMはモデルを求める際に基底関数をいくつ重ね合わせるかのパラメータとなります。
パラメータがごとのグラフを表示してみます。
前回のグラフを元にMを増加させた場合を表示させます。
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
#ボストン住宅価格データセットの読み込み
from sklearn.datasets import load_boston
def gauss( x, mu, s):
#return 1+s/(x+mu)
return npy.exp(-(x-mu)**2 / (2*s**2))
def gauss_func(w,x):
m = len(w) -1
mu = npy.linspace(0,0.5,m)
s = mu[1] -mu[0]
y = npy.zeros_like(x)
for j in range(m):
y = y + w[j]*gauss(x, mu[j], s)
y = y + w[m]
return y
def mse_gauss_func(x, t, w):
y = gauss_func(w, x)
mse = npy.mean((y-t)**2)
return mse
def fit_gauss_func(x,t,m):
mu = npy.linspace(0,0.5,m)
s = mu[1] - mu[0]
n = x.shape[0]
phi = npy.ones((n,m+1))
for j in range(m):
phi[:,j] = gauss(x,mu[j],s)
phi_T = npy.transpose(phi)
b = npy.linalg.inv(phi_T.dot(phi))
c = b.dot(phi_T)
w = c.dot(t)
return w
def show_gauss_func(w):
xb = npy.linspace(X_min, X_max, 30)
y = gauss_func(w, xb)
plt.plot(xb, y, c=[.5, .5, .5], lw=4)
boston = load_boston()
#説明変数
X_array = boston.data
#目的変数
y_array = boston.target
X = npy.array([X_array[:,0][0:40]])
Y = y_array[0:40]
xline = X[0]
yline = Y
X_min = 0
X_max = max(max(X))
X_n = len(X[0])
plt.figure(figsize=(15,7))
plt.subplots_adjust(wspace=0.3,hspace=0.4)
M = range(2,14)
for i in range(len(M)):
plt.subplot(3,4,i + 1)
W = fit_gauss_func(xline,yline,M[i])
show_gauss_func(W)
plt.plot(xline,yline,marker='o',linestyle='None',markeredgecolor='black',color='cornflowerblue')
plt.xlim(X_min, X_max)
plt.ylim(0, 50)
title = "M={0:d},SD={1:.2f}cm".format(M[i],npy.sqrt(mse))
plt.title(title)
plt.grid(True)
mse = mse_gauss_func(X[0],Y[0],W)
plt.show()・出力結果
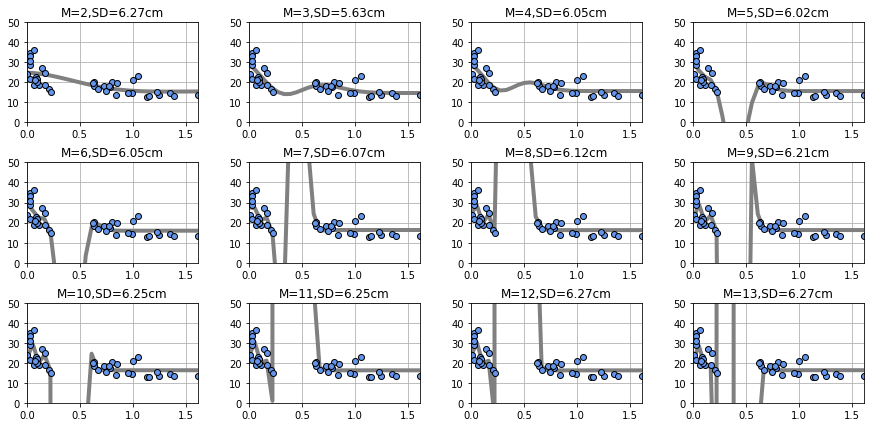
Mの値が大きくなるとプロットがない部分のグラフの描写はずれが大きくなっているように見えます。
誤差であるSDについてはM=3のところで最小となり、それ以降ではグラフの形に比べてSD値は一定になっているように見えます。
これはデータプロットがある部分では、誤差を小さくするために最適な値を選択できるようになりますが、データプロットがない部分では平均二乗誤差には関係がないため、その部分では歪みが生じている結果です。
ここで、最適なMの値を求めるのが難しくなります。
一般的にはMの値を増やすと誤差SDは小さくなる傾向にありますが、グラフの増減が大きくなるため、現在プロットがない部分のデータを予測する場合の予測値の乖離が大きくなると予測されます。
このような現象をオーバーフィッティング(過学習)と呼びます。
訓練データに沿いすぎてテストデータで求める予測がずれる状態ともいえるかもしれません。
過学習を克服したモデルを一般には汎化能力が高いモデルと呼びます。
ホールドアウト検証(モデルの検証)
前述の問題に対応するためには作成したモデルが最適なものであるかを検証する必要があります。
一般的なモデルの検証に用いられる手法の一つにホールドアウト検証と言われるものがあります。
データセットをテストデータと訓練データに任意の割合で分け、その後、モデルパラメータWを訓練データにより最適化します。
モデルパラメータWを求めることはモデルを求めることに他なりませんので、そのモデルをテストデータで評価します。
評価の際にはWに対する平均二乗誤差を算出し、検証とします。

・モデルの検証の実装
# ホールドアウト検証
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
#ボストン住宅価格データセットの読み込み
from sklearn.datasets import load_boston
def gauss( x, mu, s):
#return 1+s/(x+mu)
return npy.exp(-(x-mu)**2 / (2*s**2))
def gauss_func(w,x):
m = len(w) -1
mu = npy.linspace(0,0.5,m)
s = mu[1] -mu[0]
y = npy.zeros_like(x)
for j in range(m):
y = y + w[j]*gauss(x, mu[j], s)
y = y + w[m]
return y
def mse_gauss_func(x, t, w):
y = gauss_func(w, x)
mse = npy.mean((y-t)**2)
return mse
def fit_gauss_func(x,t,m):
mu = npy.linspace(0,0.5,m)
s = mu[1] - mu[0]
n = x.shape[0]
phi = npy.ones((n,m+1))
for j in range(m):
phi[:,j] = gauss(x,mu[j],s)
phi_T = npy.transpose(phi)
b = npy.linalg.inv(phi_T.dot(phi))
c = b.dot(phi_T)
w = c.dot(t)
return w
def show_gauss_func(w):
xb = npy.linspace(X_min, X_max, 30)
y = gauss_func(w, xb)
plt.plot(xb, y, c=[.5, .5, .5], lw=4)
boston = load_boston()
#説明変数
X_array = boston.data
#目的変数
y_array = boston.target
# 訓練データ
X = npy.array([X_array[:,0][0:40]])
Y = y_array[0:40]
# テストデータ
test_X = npy.array([X_array[:,0][121:150]])
test_Y = y_array[121:150]
xline = X[0]
yline = Y
test_xline = test_X[0]
test_yline = test_Y
X_min = 0
X_max = max(max(X))
X_n = len(X[0])
plt.figure(figsize=(15,7))
plt.subplots_adjust(wspace=0.3,hspace=0.4)
M = range(2,14)
for i in range(len(M)):
plt.subplot(3,4,i + 1)
W = fit_gauss_func(xline,yline,M[i])
show_gauss_func(W)
plt.plot(xline,yline,marker='o',linestyle='None',markeredgecolor='black',color='cornflowerblue')
plt.plot(test_xline,test_yline,marker='o',linestyle='None',markeredgecolor='black',color='white')
plt.xlim(X_min, X_max)
plt.ylim(0, 50)
title = "M={0:d},SD={1:.2f}cm".format(M[i],npy.sqrt(mse))
plt.title(title)
plt.grid(True)
mse = mse_gauss_func(test_X[0],test_Y[0],W)
plt.show()・出力結果
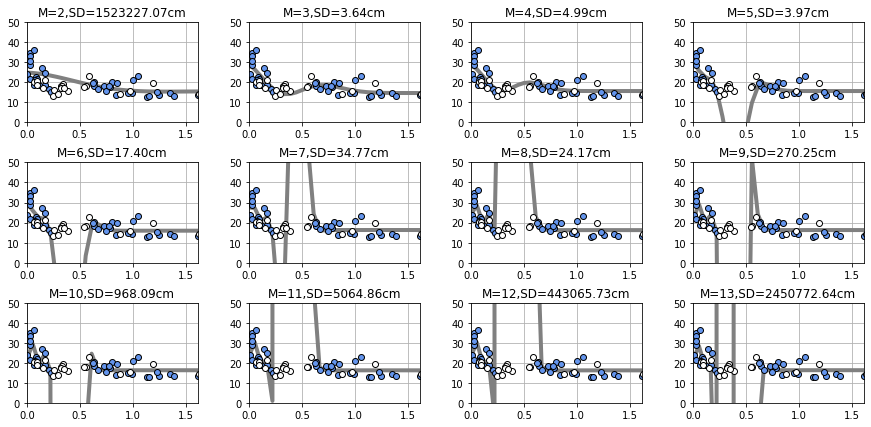
今回はデータセットの一部のデータを訓練データとして使用していたので、データセットのうち使用していなかったデータの一部をテストデータとして活用します。
上記の図では白プロットがテストデータを表し、またテストデータから誤差SDを算出しています。
今回のデータではM=3の場合がSDが最小になり最適なモデルであると判断できます。
M=6以降からSDの値が急激に大きくなっていくのが分かり、今回のパターンではここから過学習が起きていると判断できます。
つまりは訓練データに沿いすぎていてテストデータに適用したときの誤差が大きくなっていて汎用性が落ちていると分かります。
交差検証法(クロスバリデーション法)
交差検証法の実装
さきほどのホールドアウト検証により生成したモデルのうち最適なものを選択することができました。
しかしこの方法の場合、訓練データとテストデータの分割する箇所によって結果が変わってくるという性質があります。
この結果のバラつきをできるだけ少なくするための検証法が今回扱う交差検証法となります。
交差検証法ではいろいろな分割で誤差を出して平均を求める方法です。
分割をKとして設定した場合、以下のようなイメージで訓練データとテストデータを分割して検証を繰り返し最終的に誤差の平均を求めます。
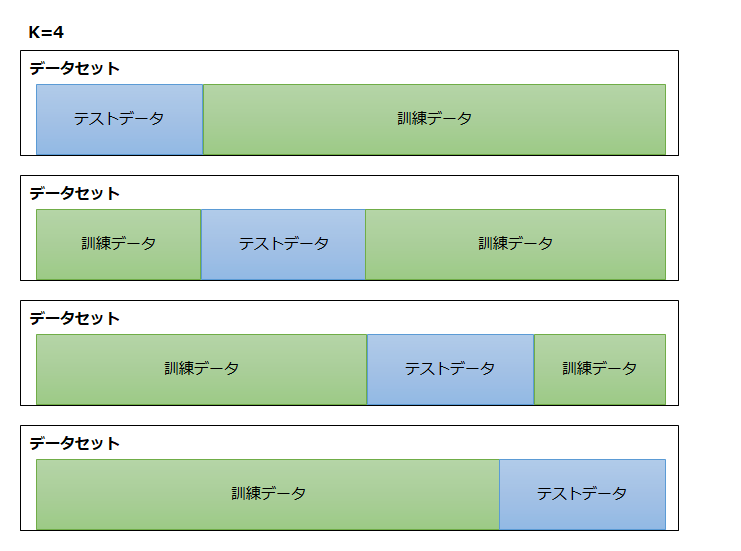
・実装例
# 交差検証法
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
#ボストン住宅価格データセットの読み込み
from sklearn.datasets import load_boston
def gauss( x, mu, s):
#return 1+s/(x+mu)
return npy.exp(-(x-mu)**2 / (2*s**2))
def gauss_func(w,x):
m = len(w) -1
mu = npy.linspace(0,0.5,m)
s = mu[1] -mu[0]
y = npy.zeros_like(x)
for j in range(m):
y = y + w[j]*gauss(x, mu[j], s)
y = y + w[m]
return y
def kfold_gauss_func(x,t,m,k):
n = x.shape[0]
mse_train = npy.zeros(k)
mse_test = npy.zeros(k)
for i in range(0, k):
x_train = x[npy.fmod(range(n), k) != i]
t_train = t[npy.fmod(range(n), k) != i]
x_test = x[npy.fmod(range(n), k) == i]
t_test = t[npy.fmod(range(n), k) == i]
wm = fit_gauss_func(x_train, t_train, m)
mse_train[i] = mse_gauss_func(x_train, t_train,wm)
mse_test[i] = mse_gauss_func(x_test, t_test, wm)
return mse_train, mse_test
def mse_gauss_func(x, t, w):
y = gauss_func(w, x)
mse = npy.mean((y-t)**2)
return mse
def fit_gauss_func(x,t,m):
mu = npy.linspace(0,0.5,m)
s = mu[1] - mu[0]
n = x.shape[0]
phi = npy.ones((n,m+1))
for j in range(m):
phi[:,j] = gauss(x,mu[j],s)[0]
phi_T = npy.transpose(phi)
b = npy.linalg.inv(phi_T.dot(phi))
c = b.dot(phi_T)
w = c.dot(t)
return w
boston = load_boston()
#説明変数
X_array = boston.data
#目的変数
y_array = boston.target
# 訓練データ
X = npy.array([X_array[:,0][0:100]])
Y = y_array[0:100]
xline = X[0]
yline = Y
X_min = 0
X_max = max(max(X))
X_n = len(X[0])
plt.figure(figsize=(15,7))
plt.subplots_adjust(wspace=0.3,hspace=0.4)
M = range(2,14)
K = 10
Cv_Gauss_train = npy.zeros((K, len(M)))
Cv_Gauss_test = npy.zeros((K, len(M)))
for i in range(0, len(M)):
Cv_Gauss_train[:, i], Cv_Gauss_test[:, i] = kfold_gauss_func(xline, yline,M[i],K)
mean_Gauss_train = npy.sqrt(npy.mean(Cv_Gauss_train, axis=0))
mean_Gauss_test = npy.sqrt(npy.mean(Cv_Gauss_test, axis=0))
plt.figure(figsize=(4,3))
plt.plot(M,mean_Gauss_train, marker='o',linestyle='-',markeredgecolor='black',color='green',label='tarining')
plt.plot(M,mean_Gauss_test, marker='o',linestyle='-',markeredgecolor='black',color='cornflowerblue',label='test')
plt.legend(loc='upper left', fontsize=10)
plt.xlim(2,6)
plt.ylim(0,500)
plt.grid(True)
plt.show()・出力結果
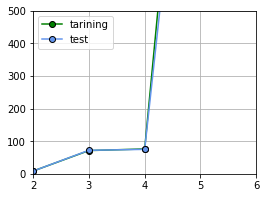
今回の結果だとM=2の場合で誤差が最小になるという結果になりました。
※あまりおもしろくはない結果かもしれませんね・・
またグラフを見るに、M=5で過学習を迎えていると判断してよさそうです。
が、もちろんデータセットの量や分割回数を表すKの値によっても結果は変わってくるのでその辺のパラメータは調整が必要です。
本来は、訓練データの誤差はテストデータよりも小さくなり、Mの値が大きくなるほど誤差は小さくなる傾向がでてくるようですが今回はそううまくはいきませんでしたね。
交差検証法の関数
交差検証法の関数として新たに「kfold_gauss_func」の関数を実装しました。
def kfold_gauss_func(x,t,m,k):
# xとtはデータセット
n = x.shape[0]
mse_train = npy.zeros(k)
mse_test = npy.zeros(k)
# 分割数Kの数だけループ
for i in range(0, k):
# データをkで分割してi番目以外を訓練データとする
x_train = x[npy.fmod(range(n), k) != i]
t_train = t[npy.fmod(range(n), k) != i]
# データをkで分割してi番目をテストデータとする
x_test = x[npy.fmod(range(n), k) == i]
t_test = t[npy.fmod(range(n), k) == i]
# 訓練データからパラメータwを求める
wm = fit_gauss_func(x_train, t_train, m)
# 訓練データとテストデータで誤差を求める
mse_train[i] = mse_gauss_func(x_train, t_train,wm)
mse_test[i] = mse_gauss_func(x_test, t_test, wm)
return mse_train, mse_test
今回の場合は上記関数の返却値を平均することでMごとの誤差を求めています。
mean_Gauss_train = npy.sqrt(npy.mean(Cv_Gauss_train, axis=0)) mean_Gauss_test = npy.sqrt(npy.mean(Cv_Gauss_test, axis=0))
M=2の場合のモデル
本来の目的は最適なMの値を求めてモデルを生成することなので、M=2でモデルを求め直します。
・実装例
# M=2の予測値
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
#ボストン住宅価格データセットの読み込み
from sklearn.datasets import load_boston
def gauss( x, mu, s):
return npy.exp(-(x-mu)**2 / (2*s**2))
def gauss_func(w,x):
m = len(w) -1
mu = npy.linspace(0,0.5,m)
s = mu[1] -mu[0]
y = npy.zeros_like(x)
for j in range(m):
y = y + w[j]*gauss(x, mu[j], s)
y = y + w[m]
return y
def mse_gauss_func(x, t, w):
y = gauss_func(w, x)
mse = npy.mean((y-t)**2)
return mse
def fit_gauss_func(x,t,m):
mu = npy.linspace(0,0.5,m)
s = mu[1] - mu[0]
n = x.shape[0]
phi = npy.ones((n,m+1))
for j in range(m):
phi[:,j] = gauss(x,mu[j],s)
phi_T = npy.transpose(phi)
b = npy.linalg.inv(phi_T.dot(phi))
c = b.dot(phi_T)
w = c.dot(t)
return w
def show_gauss_func(w):
xb = npy.linspace(X_min, X_max, 30)
y = gauss_func(w, xb)
plt.plot(xb, y, c=[.5, .5, .5], lw=4)
boston = load_boston()
#説明変数
X_array = boston.data
#目的変数
y_array = boston.target
X = npy.array([X_array[:,0][0:100]])
Y = y_array[0:100]
xline = X[0]
yline = Y
X_min = 0
X_max = max(max(X))
X_n = len(X[0])
M = 2
plt.figure(figsize=(4,4))
W = fit_gauss_func(xline,yline,M)
show_gauss_func(W)
plt.plot(xline,yline,marker='o',linestyle='None',markeredgecolor='black',color='cornflowerblue')
plt.xlim(X_min, X_max)
plt.grid(True)
mse = mse_gauss_func(X[0],Y[0],W)
title = "M={0:d},SD={1:.2f}cm".format(M,npy.sqrt(mse))
plt.title(title)
plt.show()・出力結果
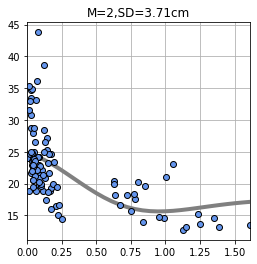
データセットの範囲を変えているという恐らくデータ分析における禁じ手をしているのであてにはならないところですが、
着目すべきは検証法によって最適なMの値が変わっているということです。
誤差SDの値もホールドアウト検証法よりも小さい値を導出することができています。
特にデータセットの数が少ない場合にはホールドアウト検証法よりも交差検証法の方が優位になる傾向があるようです。
データセット数が十分な数を用意できていれば、正常なデータ分布であればほぼ同様の結果が算出できるはずです。
・今回のソース
python_dev/Supervised_learning6.ipynb at master · wantanblog/python_dev · GitHub