深く立ち入りすぎずに今回はシグマについて(*´Σ`)
和の記号Σ
シグマ(Σ)とは
シグマ(Σ)は数列の総和を表します。
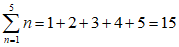
「n」という変数に1から5までの数字を入れていき、その結果を足し合わせるという要領です。
この程度の関数と数字なら、公式なんてなくてもなんとかなるしあまり意味も感じませんが、関数が複雑化したり数字が大きくなった場合にはとても一から計算していられません。
なので、公式化して利用するのが一般的でしょう。
一番ポピュラーなものは数列「n」の総和を表す公式でしょうか。
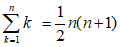
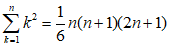
もちろんこれは基本中の基本ですが、全く数学やってないと忘れてますね。
一般的な公式自体は他にもありますが一旦ここまで。
機械学習における数学では頻出となるようです。
プログラムで記述するならfor文を使用した演算方法はどのような言語でもすぐに思いつくでしょう。
・例
import numpy as npy
# 関数k
def funck(k):
return k
# 関数k^2
def funckk(k):
return k**2
# 1から5の配列
numlist = [1,2,3,4,5]
resultk = 0
resultkk = 0
for i in numlist:
resultk = resultk + funck(i)
for i in numlist:
resultkk = resultkk + funckk(i)
print('kの和')
print(resultk)
print('k^2の和')
print(resultkk)・出力結果
kの和 15 k^2の和 55
内積をシグマで表現する
「その1」の記事で扱ったベクトルの内積はCOSを使用して求める他にも各要素を掛け合わせた総和によっても算出することができます。
・ベクトルの内積
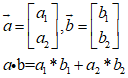
要素の総和となるため、これはシグマ(Σ)を使用して以下のように表現することも可能です。
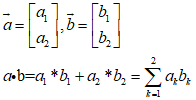
Pythonでは内積用の関数がありますので、先ほどと同様の演算を内積を求める「dot」を使用することで表現できます。
但し各要素をベクトルで表現する必要があります。
・例
import numpy as npy
# 関数k
def funck(k):
return k
# 関数k^2
def funckk(k):
return k**2
# 1から5の配列
ones = npy.ones(5)
numlist = npy.arange(1,6)
klist = funck(numlist)
kklist = funckk(numlist)
resultk = ones.dot(klist)
resultkk = ones.dot(kklist)
print('kの和')
print(resultk)
print('k^2の和')
print(resultkk)・出力結果
kの和 15.0 k^2の和 55.0
この表現であれば、関数が複雑した場合でも対応できる場合があります。
・例
import numpy as npy
# 関数a
def func1(k):
return 2*k
# 関数b
def func2(k):
return k**2 + k +1
# 1から20の配列
numlist = npy.arange(1,21)
list1 = func1(numlist)
list2 = func2(numlist)
result = list1.dot(list2)
print('2k(k^2+k+1)の1から20までの総和')
print(result)・出力結果
2k(k^2+k+1)の1から20までの総和 94360
なにをやっているかと言えば上記の公式中のベクトルa=2kとしてベクトルb=(k^2+k+1)である場合に、kが1から20まで変化する場合の総和を求めています。
この例だと一つの関数にして求めることもできますが、それぞれの関数が完全に独立したものである場合にも同様の方法で求めることができます。
パイ(Π)積の記号
総和を求めるシグマと同列のものが積の記号Π です。シグマと同様に全ての数字を掛けていき総乗を算出します。
私自身は数学で記号自体を扱ったことはまともにありませんね。
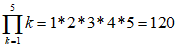
プログラムではある程度数字が大きくなっても実装は普通にできるのでループを使えばとりあえず表現することは可能です。
もっと賢そうな書き方もあるでしょうが・・・
・例
import numpy as npy
# 関数k
def funck(k):
return k
# 関数2
def func2(k):
return k**2 + 2*k
# 1から5の配列
numlist = [1,2,3,4,5]
resultk = 1
resultkk = 1
for i in numlist:
resultk = resultk * funck(i)
for i in numlist:
resultkk = resultkk * func2(i)
print('kの総乗')
print(resultk)
print('k^2+2kの総乗')
print(resultkk)・出力結果
kの総乗 120 k^2+2kの総乗 302400
短いですが今回はここまで
今回のソース
python_dev/Python_math2.ipynb at master · wantanblog/python_dev · GitHub