回帰編の基本は今回で完了する予定です。
モデルを考えてみる
データセットに対する最適なグラフの形は?
前回のデータセットでは交差検証法により以下のようなモデルを生成しました。
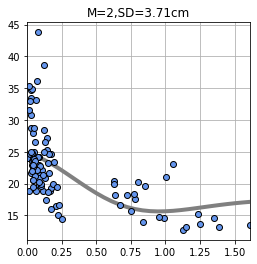
元々このデータは横軸は人口 1 人当たりの犯罪発生数、縦軸が所有者が占有している家屋の$ 1000単位の中央値だったので縦軸は一定の値に収束することが予測できます。
なので、上記のモデルのように途中から上がることは考えにくく、一定の値以降は収束するような以下のモデルになるのではないかと常識的な知識で予測できます。

ここでモデルに適切そうな関数モデルを考えてみます。
・関数モデルの選定
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f1(x):
return npy.exp(x)
def f2(x):
return npy.exp(-x)
def f3(x):
return -npy.exp(x)
def f4(x):
return -npy.exp(x)
# X軸に0から9までの配列
xline = npy.linspace(-5,5,50)
yline1 = f1(xline)
yline2 = f2(xline)
yline3 = f3(xline)
yline4 = f4(xline)
# pltに要素を設定する
plt.plot(xline, yline1, color ='black', label='$w=1$')
plt.plot(xline, yline2, color ='red', label='$w=2$')
plt.plot(xline, yline3, color ='blue', label='$w=3$')
plt.plot(xline, yline4, color ='green', label='$w=4$')
# 凡例を表示する
plt.legend(loc="upper left")
# y軸の表示範囲を設定する
plt. ylim(- 50, 50)
# タイトルを表示する
plt.title('$SampleGraph$')
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
# グリッドを表示する
plt.grid(True)
# グラフを描写する
plt.show()・出力結果

グラフの形としては二つ目の指数関数のグラフと形が近いことが分かり、このグラフに切片を加えることで想定したモデルに近づきます。
・想定モデル
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f2(x):
return 1 + 5*npy.exp(-x)
# X軸に0から9までの配列
xline = npy.linspace(0,5,50)
yline2 = f2(xline)
# pltに要素を設定する
plt.plot(xline, yline2, color ='red', label='$w=2$')
# 凡例を表示する
plt.legend(loc="upper left")
# y軸の表示範囲を設定する
plt. ylim(0, 10)
# タイトルを表示する
plt.title('$SampleGraph$')
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
# グリッドを表示する
plt.grid(True)
# グラフを描写する
plt.show()・出力結果

このような関数を適用するとそれらしいモデルの形が設定できそうです。
オリジナルモデルの作成
オリジナルモデルの実装
まずは実装を行います。モデルは以下を適用します。

・モデル実装
# オリジナルモデル
import numpy as npy
import matplotlib.pyplot as plt
from scipy.optimize import minimize
%matplotlib inline
#ボストン住宅価格データセットの読み込み
from sklearn.datasets import load_boston
# モデル関数
def model_func(x, w):
y = w[0] + w[1] * npy.exp(-w[2]*x)
return y
# モデルのグラフ表示
def show_model_func(w):
xb = npy.linspace(X_min, X_max, 100)
y = model_func(xb, w)
plt.plot(xb, y, c=[.5, .5, .5],lw=4)
# MSEの導出
def mse_model_func(w, x, t):
y = model_func(x, w)
mse = npy.mean((y - t)**2)
return mse
# 最適化パラメータの導出
def fit_model_func(w_init, x, t):
result = minimize(mse_model_func, w_init, args=(x,t),method="powell")
return result['x']
boston = load_boston()
#説明変数
X_array = boston.data
#目的変数
y_array = boston.target
X = npy.array([X_array[:,0][0:100]])
Y = y_array[0:100]
xline = X[0]
yline = Y
X_min = min(xline)
X_max = max(xline)
plt.figure(figsize=(4,4))
W_init=[10, 1 ,0]
W = fit_model_func(W_init, xline, yline)
print("w0={0:.1f}, w1={1:.1f},w2={2:.1f}".format(W[0],W[1],W[2]))
show_model_func(W)
plt.plot(xline,yline,marker='o',linestyle='None',markeredgecolor='black',color='cornflowerblue')
plt.grid(True)
mse = mse_model_func(W, xline, yline)
print("SD={0:.2f}cm".format(npy.sqrt(mse)))
plt.show()・出力結果
w0=16.4, w1=12.0,w2=5.6
SD=4.62cm

ライブラリscipy.optinize
今回は最適パラメータwを求めるためにライブラリを活用しました。
Pythonのscipy.optinizeのminimize関数により求めています。
result = minimize(mse_model_func, w_init, args=(x,t),method="powell")
第一引数にモデル関数のmse_model_func。
第二引数にデータセット。
第三引数に最適化手法をそれぞれ設定します。
ここでの最適化手法のpowell法は最適化手法の一つです。
非線形連立方程式の解、あるいは連続最適化問題の関数の極大・極小解を見つけるためのアルゴリズムである
モデル関数
グラフの形を決める関数です。
# モデル関数
def model_func(x, w):
y = w[0] + w[1] * npy.exp(-w[2]*x)
return y
モデルのグラフ表示
モデル関数のグラフ描写用の関数です。
# モデルのグラフ表示
def show_model_func(w):
xb = npy.linspace(X_min, X_max, 100)
y = model_func(xb, w)
plt.plot(xb, y, c=[.5, .5, .5],lw=4)
MSEの導出
当該関数のMSE(誤差)を導出するための関数です。
# MSEの導出
def mse_model_func(w, x, t):
y = model_func(x, w)
mse = npy.mean((y - t)**2)
return mse
最適化パラメータの導出
先ほどのライブラリを用いたパラメータの導出関数です。
# 最適化パラメータの導出
def fit_model_func(w_init, x, t):
result = minimize(mse_model_func, w_init, args=(x,t),method="powell")
return result['x']
結果としては
出力結果を再掲します。
w0=16.4, w1=12.0,w2=5.6
SD=4.62cm

グラフの形としてはかなりそれらしい形になりました。
SDは4.62cmで、前回のガウス関数を用いたモデルよりは値は大きくなっているので、今回のデータセットとしては前回のモデルの方が優れていると判断できるようです。
このようにデータの散布図からのモデルの概形が予測できる場合には自身で関数を考えて適用してみるような手法もあるようです。
また、自身で考えたモデルに対しても前回のガウス関数のモデルのように検証を行うのは有効です。
さて、長らく続きましたが回帰編は一旦これで終了とします。
まぁもちろん全然深くまではやり切れていないですが、基本的な流れは少しは分かったかなと思います。
次回以降は教師あり学習の中の「分類」を扱う予定です。
・今回のソース
python_dev/Supervised_learning7.ipynb at master · wantanblog/python_dev · GitHub