何も分からなかった状態の基礎編、重く苦しい数学編をなんとか超えてついに機械学習編にたどり着きました!
基本も数学も適宜振り返る必要があると思われ、何も分からなくて苦しいのは今後も続くと見込まれますが、とにかく本編がやっとスタートします。
教師あり学習とは
教師あり学習については過去の記事で以下のように触れました。
教師あり学習とは、「入力」とそれに対する「正しい出力」がセットになった訓練データをあらかじめ用意して、コンピュータに学習させる方法
引用元:マンガでわかる! 人工知能 AIは人間に何をもたらすのか
そもそも教師あり学習とは、人口知能アルゴリズムを教師あり学習と教師なし学習で分類したときの一つになります。
教師あり学習は、正解ラベルのついたデータセットを用意し、それを学習させることにより、人口知能モデルをつくることとなります。
また、教師あり学習はさらに大きく分類問題と回帰問題に大別されます。
今回のテーマは回帰です。
機械学習における回帰は統計学における回帰とほぼ等価と捉えて問題なさそうです。
つまりここで言う回帰とは、数値を予測することになります。
データセットから特定の規則を探し出し、結果を予想することになります。
最も単純なケースでは、複数のプロットから一次関数を導きだし(線形回帰)、xからyの値を求めるようなことになると思われます。
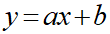
データセット
線形回帰モデルは、現時点では特定のデータセットから関数を導出したモデルと捉えています。
まずはサンプルとしてデータセットを用意します。
データセットを用意する
今回はリソース数は少ないですが、本ブログを題材にしたいと思います。
Googleアナリティクスよりページビュー数とユーザ数を取得してその関係を扱ってみます。
データはどっかのDBに保存して解析できるようにしたいけどそれはいずれかなぁ。
・例
import numpy as npy
# データ生成
xnum = 8
views =[235,375,568,931,1497,1542,3176,1084]
users =[24,93,154,370,746,868,1809,699]
# データをblog_data.npzファイルに保存する
npy.savez('blog_data.npz',X=views,X_min=min(views),X_max=max(views),X_n=len(views),Y=users)
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('blog_data.npz')
print(sample_data['X'])
print(sample_data['X_min'])・出力結果
[ 235 375 568 931 1497 1542 3176 1084] 235
上記例では「npy.savez」によりデータを「.npz」ファイルに保存しています。
保存したファイルは対象ソースが存在するフォルダ(ディレクトリ)に保存され、以降いつでもデータを読み込むことができます。
読込みは「npy.load」により行い、「.npz」形式で保存している場合にはロードしたデータはJSON形式に似た扱い方でそれぞれのデータを取り出すことができます。
もし適切なデータがない場合は、ランダムで適当な数値を生成すればよいでしょう。
データセットのグラフを表示する
生成したデータセットをグラフ上に散布図で表現してみます。
・例
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('blog_data.npz')
plt.figure(figsize=(4,4))
plt.plot(sample_data['X'],sample_data['Y'],marker='o',linestyle='None',markeredgecolor='black',color='cornflowerblue')
plt.xlim(sample_data['X_min'],sample_data['X_max'])
plt.grid(True)・出力結果
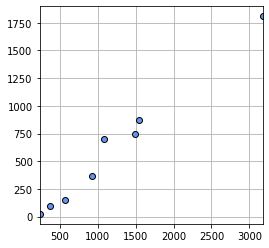
図表上のプロットは「plt.plot」により行います。
うーん、ちょっと規則性が高すぎる気がしてデータとしては題材としてはあまりよくなかったかな?
最小二乗法
線形回帰モデルを求める方法としては、「最小二乗法」と言われる方法が有名です。
ここでは、Pythonで最小二乗法を理解しながら、プログラミングによりそれらしい概ねの結果を求めてみたいと思います。
最小二乗法をPythonで理解する
今、何がしたいかと言うとプロットを行ったデータから、最もらしい一次関数を求めることです。
つまりは以下の式の傾き「w0」と切片「w1」を求めることになります。
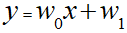
最小二乗法は誤差Jを以下の式により表します。
意味は後からひも解いてみます。
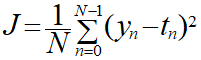
ここでも「yn」は「y=w0x+w1」で表せられるn番目の一次関数のことで以下の通り表現されます。
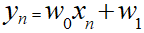
w0とw1は重みと言われるもので、これらが決まると誤差Jを求めることができます。
w0及びw1とJの関係性をグラフにより図示してみます。
・例
import numpy as npy
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# 平均誤差関数
def mse_line(x,t,w):
y = w[0]*x + w[1]
# 要素の平均を求める
mse = npy.mean((y-t)**2)
return mse
# データの読み込み
sample_data = npy.load('blog_data.npz')
# データの計算
xn = 100
w0_range = [-5, 5]
w1_range = [-1000, 1000]
w0 = npy.linspace(w0_range[0],w0_range[1],xn)
w1 = npy.linspace(w1_range[0],w1_range[1],xn)
# グリッドを作成する
ww0, ww1 = npy.meshgrid(w0, w1)
J = npy.zeros((len(w0), len(w1)))
for i0 in range(len(w0)):
for i1 in range(len(w1)):
J[i1, i0] = mse_line(sample_data['X'],sample_data['Y'],(w0[i0], w1[i1]))
# 表示
plt.figure(figsize=(9.5, 4))
plt.subplots_adjust(wspace=0.5)
ax = plt.subplot(1,2,1,projection='3d')
ax.plot_surface(ww0, ww1, J, rstride=10, cstride=10, alpha=0.3, color='blue', edgecolor='black')
ax.set_xticks([-10, 0, 10])
ax.set_yticks([-1000, 0, 1000])
ax.set_zticks([0, 10000000, 100000000])
ax.view_init(20, 60)
plt.subplot(1,2,2)
cont = plt.contour(ww0, ww1, J, 30, colors='black', levels=[100000, 1000000, 10000000])
cont.clabel(fmt='%d', fontsize=8)
plt.grid(True)
plt.show()・出力結果
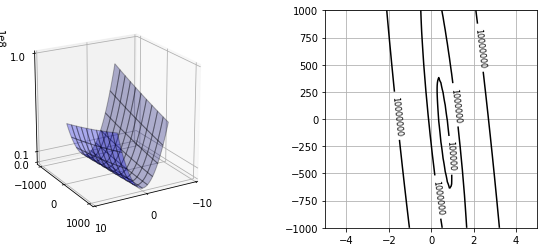
なにをやっているか分かるでしょうか?
私は以下の値をいじっているうちに何となく分かってきました。
w0_range = [-5, 5] w1_range = [-1000, 1000]
これは何を表しているのでしょうか。少し考えてみましょう。
そもそも最小二乗法はグラフ上の以下を表しています。
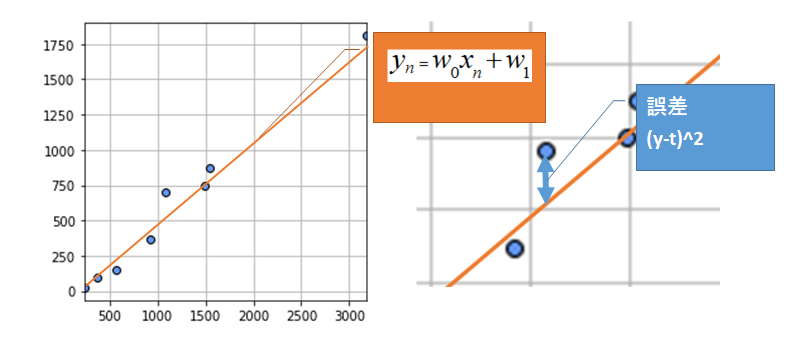
ここでは元のデータのプロットの縦の大きさを「t」として直線の縦の大きさを「y」としています。
つまり(y-t)は学習データのプロットと直線の距離を表しているということになります。
プロットは直線に対して上にずれたり、下にずれたりするため、そのままとるとプラスとマイナスの値が混ざってしまうため全て正の数として扱うために2乗しています。
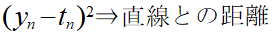
そして、Σを使用することで全プロットと直線の距離合計を求めていることになります。
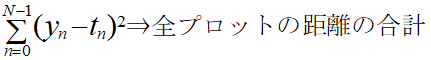
そしてこれに「1/N」をかける、つまり要素の数で割っていることに等しいので平均を求めていることになります。
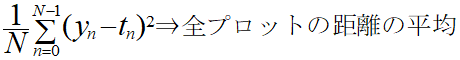
つまりこれがこれまで誤差と呼んでいたJの正体ということになります。
全てのプロットが直線上に存在する場合を求められるならばこの値はゼロになります。
最小二乗法とは、この誤差Jが最小になるw0とw1の組み合わせを探す方法です。
今回は参考書に沿って平均値で求めていますが、単なる合計値で求めたとしても最小になる点というのは変わらないので、平均をとらない場合もあるということです。
ここまでくると分かってきます。
上記のPythonプログラムでは以下の範囲で、直線を生成していき誤差を調べています。
w0_range = [-5, 5] w1_range = [-1000, 1000]
このことから、三次元のグラフや高等線から、誤差Jが最小になりそうなポイント(w0とw1の組み合わせ)がなんとなく分かるわけです。
高さの軸が一番小さいところが今求めているポイントです。
これは高等線が分かりやすく、一番小さい範囲に合わせて「w0とw1の範囲」を調整していくとさらに詳細が分かってくるわけです。
どうでしょうか?なんとなく伝わりましたかね?
Pythonで概ねの値を求める
先ほどの最小二乗法のプログラムを用いて、概ねの答えを求めてみましょう。
・例
import numpy as npy
# 平均誤差関数
def mse_line(x,t,w):
y = w[0]*x + w[1]
# 要素の平均を求める
mse = npy.mean((y-t)**2)
return mse
# データの読み込み
sample_data = npy.load('blog_data.npz')
# データの計算
xn = 100
w0_range = [-5, 5]
w1_range = [-1000, 1000]
w0 = npy.linspace(w0_range[0],w0_range[1],xn)
w1 = npy.linspace(w1_range[0],w1_range[1],xn)
# グリッドを作成する
ww0, ww1 = npy.meshgrid(w0, w1)
J = npy.zeros((len(w0), len(w1)))
min_J = 10000
min_w0 = 0
min_w1 = 0
for i0 in range(len(w0)):
for i1 in range(len(w1)):
J[i1, i0] = mse_line(sample_data['X'],sample_data['Y'],(w0[i0], w1[i1]))
if min_J > J[i1, i0]:
min_J = J[i1, i0]
min_w0 = w0[i0]
min_w1 = w1[i1]
print('Jの最小値')
print(min_J)
print('w0 = '+str(min_w0) +', w1 = ' + str(min_w1))・出力結果
Jの最小値 6290.442467605344 w0 = 0.6565656565656566, w1 = -171.71717171717182
誤差Jの最小値を探し、そのときのw0とw1 を記録しています。
あくまで、今回試している範囲と粒度にはなりますが、一応答えらしきものを算出することができました。
求めた関数をデータプロット上に図示してみます。
・例
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
# 最小二乗法により求めた関数
def f(x):
return 0.6565656565656566*x -171.71717171717182
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('blog_data.npz')
plt.figure(figsize=(4,4))
plt.plot(sample_data['X'],sample_data['Y'],marker='o',linestyle='None',markeredgecolor='black',color='cornflowerblue')
plt.xlim(sample_data['X_min'],sample_data['X_max'])
# 一次関数の図示する
xline = npy.linspace(sample_data['X_min'],sample_data['X_max'],100)
yline1 = f(xline)
plt.plot(xline, yline1, color ='orange')
# X軸に名前を付ける
plt.xlabel('$views$')
# Y軸に名前を付ける
plt.ylabel('$users$')
plt.grid(True)・出力結果
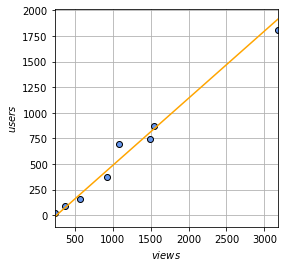
グラフ上で見ても概ね正しそうであることが分かります。
つまりはこの関数からビュー数とユーザ数の相関関係が分かりますので、例えばページビュー数が10000回の場合、どの程度のユーザに見てもらえることになるかを推測することができます。
・例
import numpy as npy
# 最小二乗法により求めた関数
def f(x):
return 0.6565656565656566*x -171.71717171717182
xline = npy.array([1000,5000,10000,20000,30000])
yline = npy.round(f(xline))
print('ページビュー数')
print(xline)
print('ユーザ数')
print(yline)・出力結果
ページビュー数 [ 1000 5000 10000 20000 30000] ユーザ数 [ 485. 3111. 6394. 12960. 19525.]
ページビュー数が10000回となるのは私のブログの場合はユーザ数6394人が必要になると推測できます。
厳密に求める最小二乗法
数学的な解法
上記の方法でもそれらしい線形回帰モデルを求めることができました。
しかし今回の方法では、あくまで今回用意したw0とw1の組み合わせから最も誤差が小さいものを選択した形となっています。
つまりは全パターンの中から厳密な組み合わせを求めることができていません。
線形回帰などの考えは数学的な根拠に基づいていますので、数学的に求めることはもちろん可能です。
ここでは詳細な計算は省きますが、その流れと考え方だけ示してみたいと思います。
式は上記を元に以下を用います。
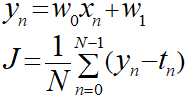
ここで「y」を置き換えると以下のようになります。
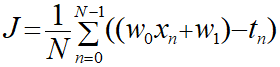
xとtは自分が用意したデータセットから値を代入することができます。
n=0のときは「x=235、t=24」といった具合にn=7までの値を入れることができ、今回のケースではこれが8つ並ぶことになります。
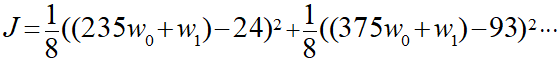
この計算を進めるのはしんどいので今回は行いませんが、重要なのは誤差Jを変数w0とw1の式として表現できるということです。
ここで、誤差Jが最小になるw0とw1の組み合わせを求めるために何をするのかというとw0とw1のそれぞれで偏微分を行います。
w0とw1のそれぞれで偏微分した結果が0になる場合を求めます。0になる場合というのはつまり誤差Jが最小になるときです。
偏微分がしっくりこなくても、二次関数の微分で最小を求めるときと同じようなものなんだなぁと思えばよいと思います。
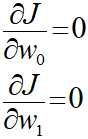
ここまでやっても変数w0とw1が残ったままですが、2本の式に変数2つということで連立方程式の問題に落とし込むことができ、数学的なアプローチにより最適な答えを導くことができるということが分かります。
今回のサンプルデータレベルでも実際に解くのはなかなかしんどいと思います。
実用レベルのことを考え、データセットの個数が増えたり、そもそも要素が「w0、w1、w2、w3・・・」と増えていくと手動で解くのは現実的とは言えないと思います。
プログラムを中心に据えて取り組む場合にはこれを頑張って解くというよりは、重要なのは中で何に基づき何をやっているか、どのようなものを求めているのかを知っておくことではないかと思っています。
ライブラリを用いた最小二乗法
苦労した後には楽をしましょう。
この苦労が本当に必要かは私からは判断できませんが、ただ使用するよりは格段の感動が味わえます。
最小二乗法の解は「numpy.linalg.lstsq」関数を用いることで傾きw0と切片w1が求められるようです。
・例
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('blog_data.npz')
plt.figure(figsize=(4,4))
plt.plot(sample_data['X'],sample_data['Y'],marker='o',linestyle='None',markeredgecolor='black',color='cornflowerblue')
plt.xlim(sample_data['X_min'],sample_data['X_max'])
# 一次関数の図示する
X = sample_data['X']
X = np.array([X, npy.ones(len(X))])
X = X.T
w0,w1 = npy.linalg.lstsq(X,sample_data['Y'].tolist())[0]
w0 = npy.round(w0,3)
w1 = npy.round(w1,3)
xline = npy.linspace(sample_data['X_min'],sample_data['X_max'],100)
plt.plot(xline, w0*xline+w1, color ='orange')
# X軸に名前を付ける
plt.xlabel('$views$')
# Y軸に名前を付ける
plt.ylabel('$users$')
plt.grid(True)
print('y = '+str(w0)+'x + ' +str(w1))・出力結果
y = 0.617x + -130.731
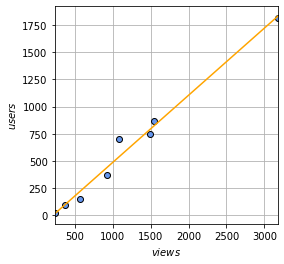
用意された関数なので、注意点としては引数と戻り値の形が決まっていることでしょうか。
これによりかなり簡単に最小二乗法の解を求めることができるようになりました。
・今回のソース
python_dev/Supervised_learning1.ipynb at master · wantanblog/python_dev · GitHub