今回も線形回帰について、線形回帰モデルを求めるために前回は最小二乗法という方法について学びましたが、今回は勾配降下法について学びます。
Pythonで学ぶ勾配降下法
線形回帰モデルを求めるために今回は勾配降下法(最急降下法)について学んでいきます。
Pythonで実装する勾配降下法
今回は実装例から入りたいと思います。
やっていることや理論については後から追っていきたいと思います。
・例
import numpy as npy
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# 平均誤差関数
def mse_line(x,t,w):
y = w[0]*x + w[1]
# 要素の平均を求める
mse = npy.mean((y-t)**2)
return mse
# 勾配
def dmse_line(x,t,w):
y = w[0]*x + w[1]
d_w0 = 2*npy.mean((y-t)*x)
d_w1 = 2*npy.mean(y-t)
return d_w0, d_w1
# 勾配法関数
def fit_line_func(x,t):
# 初期パラメータ
w_init = [1, 1]
# 学習率
alphax = 0.0000002
alphay = 0.002
max_roop = 100000
eps = 0.1
w_hist = npy.zeros([max_roop, 2])
w_hist[0,:] = w_init
for num in range(1, max_roop):
dmse = dmse_line(x,t,w_hist[num -1])
w_hist[num, 0] = w_hist[num-1,0] - alphax*dmse[0]
w_hist[num, 1] = w_hist[num-1,1] - alphay*dmse[1]
if (max(npy.isnan(npy.absolute(dmse)))):
print(w_hist[num -3])
break
if max(npy.absolute(dmse)) < eps:
break
w0 = w_hist[num, 0]
w1 = w_hist[num, 1]
w_hist = w_hist[:num,:]
return w0, w1, dmse, w_hist
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('blog_data.npz')
plt.figure(figsize=(4,4))
# MSEの等高線表示
xn = 100
w0_range = [-2, 2]
w1_range = [-140, 10]
w0 = npy.linspace(w0_range[0],w0_range[1],xn)
w1 = npy.linspace(w1_range[0],w1_range[1],xn)
# グリッドを作成する
ww0, ww1 = npy.meshgrid(w0, w1)
J = npy.zeros((len(w0), len(w1)))
for i0 in range(len(w0)):
for i1 in range(len(w1)):
J[i1, i0] = mse_line(sample_data['X'],sample_data['Y'],(w0[i0], w1[i1]))
cont = plt.contour(ww0, ww1, J, 30, colors='black', levels=[1000,10000,100000, 1000000, 10000000])
cont.clabel(fmt='%1.0f', fontsize=8)
plt.grid(True)
# 勾配法
W0, W1, dMSE, W_history = fit_line_func(sample_data['X'],sample_data['Y'])
print(W_history.shape[0])
print('w0=[{0:.6f}], w1=[{1:.6f}]'.format(W0, W1))
print('dMSE=[{0:.6f},{1:.6f}]'.format(dMSE[0],dMSE[1]))
print('MSE={0:.6f}'.format(mse_line(sample_data['X'], sample_data['Y'], [W0, W1])))
plt.plot(W_history[:,0],W_history[:,1], '.-',color='gray',markersize=10, markeredgecolor='cornflowerblue')
plt.show()・出力結果
5950 w0=[0.617423], w1=[-130.705293] dMSE=[-0.099914,0.018306] MSE=5078.154092

最小二乗法と同様に以下の一時関数のw0とw1を求めています。
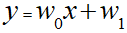
前回ライブラリによる求めた結果は以下なので、ほぼ同様の結果が得られていると言ってよさそうです。
y = 0.617x + -130.731
簡単に言うと初期パラメータを(1.1)として、そこから勾配に沿って位置を徐々にずらしていき最適な解を求めているという具合です。
ここで苦労したのがパラメータである学習率の設定です。
ここが苦労すべきところなのかどうかがいまいち分からないのですが、今回の私が用意したデータだと参考書通りでは値が発散し、うまく値が求められませんでした。
※知識不足で何が悪いのか分からず調整に一晩かかりました。
# 学習率
alphax = 0.0000002
alphay = 0.002今回は結局上記の通りとしました。学習率が適切に設定されていれば初期値がなんであってもだいぶ正確に求められるようです。
では、興味がある方は一緒にやっていることを読み解いていきましょう。
勾配のイメージをつかむ
ここでいう勾配とはなんのことなのかまずはそのイメージを掴みましょう。
以前実装した3Dグラフの表示範囲と角度を変えて表示してしました。
・例
import numpy as npy
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# 平均誤差関数
def mse_line(x,t,w):
y = w[0]*x + w[1]
# 要素の平均を求める
mse = npy.mean((y-t)**2)
return mse
# データの読み込み
sample_data = npy.load('blog_data.npz')
# データの計算
xn = 100
w0_range = [-3, 3]
w1_range = [-100, 100]
w0 = npy.linspace(w0_range[0],w0_range[1],xn)
w1 = npy.linspace(w1_range[0],w1_range[1],xn)
# グリッドを作成する
ww0, ww1 = npy.meshgrid(w0, w1)
J = npy.zeros((len(w0), len(w1)))
for i0 in range(len(w0)):
for i1 in range(len(w1)):
J[i1, i0] = mse_line(sample_data['X'],sample_data['Y'],(w0[i0], w1[i1]))
# 表示
plt.figure(figsize=(9.5, 4))
plt.subplots_adjust(wspace=0.5)
ax = plt.subplot(1,2,1,projection='3d')
ax.plot_surface(ww0, ww1, J, rstride=10, cstride=10, alpha=0.3, color='blue', edgecolor='black')
ax.set_xticks([-1, 0, 1])
ax.set_yticks([-100, 0, 100])
ax.set_zticks([0, 10000000, 20000000])
ax.view_init(40, 70)
plt.grid(True)
plt.show()・出力結果

グラフ上に一点を取ったときの見た目上の傾斜度がそのままの勾配になります。

勾配法とはこの勾配に沿って進めていき、勾配が最小になる点を探していたのです。
では、この勾配は求められるものなのでしょうか。
勾配を求める
勾配という言葉は実は過去の記事でも扱っています。
数学を扱ったときの勾配ベクトルです。
勾配ベクトルは以下の通りで偏微分を用いるのでした。

今回は誤差Jのグラフを表示していますので、誤差Jに対する偏微分を行います。

つまり勾配ベクトルは次のようになります。

Pythonで言うと以下が勾配を表現している部分にあたります。
# 勾配
def dmse_line(x,t,w):
y = w[0]*x + w[1]
d_w0 = 2*npy.mean((y-t)*x)
d_w1 = 2*npy.mean(y-t)
return d_w0, d_w1xとtにそれぞれサンプルのデータが入ります。
1/NとΣによる総和をmeanで平均として表現しているわけです。
これで勾配が求められていることが分かりました。
次はこれにより勾配から次の点を求めていきます。
勾配を利用し底を求める
勾配をたどって最小点を求めることはグラフ上では「底」を求めていることに等しいです。
次にある点(初期値)から勾配を利用して底に近づけていきます。
勾配ベクトルはそのままの状態で勾配の方向と大きさを示しています。
なので、底方向に進めていくためにはマイナスの値する必要があります。
ある点から勾配ベクトルに沿って次の点に進むのは以下の式により表現されます。

ここの「α」が先ほど苦労したといった学習率をというものです。
ここまでの経緯で、学習率が適切でないと元の点からの移動距離が大きすぎて様々な点をいったりきたりして発散してしまっていたのだと予測できます。
Pythonの実装では以下の部分にあたります。
dmse = dmse_line(x,t,w_hist[num -1])
w_hist[num, 0] = w_hist[num-1,0] - alphax*dmse[0]
w_hist[num, 1] = w_hist[num-1,1] - alphay*dmse[1]これをfor文で繰り返すことにより、座標を勾配に沿ってずらしていたということです。
「dmse」は勾配を表しているので、底に近づけば近づくほど勾配が小さくなると予測されますので、勾配が十分に小さくなったときに演算を打ち切るのが以下の部分です。
if max(npy.absolute(dmse)) < eps:
break「absolute」は絶対値を求める関数です。
これでPythonによる勾配降下法の意味が概ね読みとれたのではないかと思います。
最後に求めた回帰モデルをデータプロット上に示しておきます。
・例
import numpy as npy
import matplotlib.pyplot as plt
%matplotlib inline
# 最小二乗法により求めた関数
def f(x):
return 0.617423*x -130.705293
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('blog_data.npz')
plt.figure(figsize=(4,4))
plt.plot(sample_data['X'],sample_data['Y'],marker='o',linestyle='None',markeredgecolor='black',color='cornflowerblue')
plt.xlim(sample_data['X_min'],sample_data['X_max'])
# 一次関数の図示する
xline = npy.linspace(sample_data['X_min'],sample_data['X_max'],100)
yline1 = f(xline)
plt.plot(xline, yline1, color ='orange')
# X軸に名前を付ける
plt.xlabel('$views$')
# Y軸に名前を付ける
plt.ylabel('$users$')
plt.grid(True)・出力結果

但しの今回用いた勾配降下法では必ずしも最適な点が求められているとは限りません。
なぜなら今回の方法では初期値から最も近い底を求めているため、複数の底が存在する場合は初期値によって結果が変わってくると理解できると思います。
以下は用意がしやすい二次元グラフで考えていますが、三次元グラフであっても同じことです。

実用レベルの機械学習ではいくつもの初期値から分析を行うようです。
平均二乗誤差と標準偏差
上記の流れから平均二乗誤差について考えてみます。
最初に示した出力結果での以下が平均二乗誤差にあたります。
MSE=5078.154092
これは文字通り誤差の二乗を表していますので、感覚的にも分かりやすくするために平方根(ルート)をとります。
・例
# ライブラリのインポート import numpy as npy result = npy.sqrt(5078.154092) print(round(result,2))
・出力結果
71.26
この値がいわゆる標準偏差(SD)と言われているものです。
SD=71.26は求めた関数とデータプロットとの誤差距離を表しています。
比較的数値が大きめのデータをつかっていますのでまぁ妥当なのかもしれません。
うん、難しいなかなか進まない・・
・今回のソース
python_dev/Supervised_learning2.ipynb at master · wantanblog/python_dev · GitHub