ものすごーく久しぶりになってしまいましたが、機械学習をやります。なんとかこの本だけは完走したい。
今回の一連の機械学習の最終項として「教師なし学習」を扱います。
教師なし学習
これまでは訓練データに正解データがついたデータを扱ってきましたが、今回の「教師なし学習」では正解データがついていないデータを扱います。
■クラスタリング
教師なし学習にもいくつか種類がありますが、今回はクラスタリングを扱います。
クラスタリングは名前から教師あり学習の「分類」とも似たような印象をうけますが、クラスタリングは「クラスター」からきており、分類ではデータを予め決められたクラスに分けるのに対して、クラスタリングではデータの(特徴に応じた)集まりを見つけるような手法となります。
クラスタリングの手法にもいくつか種類があるようですが、今回は一般的な手法として知られている「K-means法」について学びます。
K-means法
概要とイメージ
k平均法(kへいきんほう、英: k-means clustering)は、非階層型クラスタリングのアルゴリズム。クラスタの平均を用い、与えられたクラスタ数k個に分類することから、MacQueen がこのように命名した。k-平均法(k-means)、c-平均法(c-means)とも呼ばれる
引用元:k平均法 - Wikipedia
初学者だと何を言っているか良く分からないですね。
クラスタリングにおける分類グループはクラスターと呼ばれています。
K-means法では、クラスター数を予め決めてから処理を行うことになります。
処理の中では、クラスターの中心ベクトルであるμ(ミュー)とクラス指示変数Rを扱うことになります。μは中心ベクトルという言い方をしていますが、グラフ上の座標を表すので(x,y)のような値が入り、Rはデータプロットがどのクラスターに所属するかを示すものなのでクラスターに応じてA、Bのような分類が入ることになります。
これらの値を相互に更新していくことによって最終的なクラスタリングを行うことになります。
私は以下のようなものとイメージしました。
イメージ図上の位置関係などは適当です。
①初期値の設定
データプロット上に任意のクラスター中心ベクトルμを設定する。
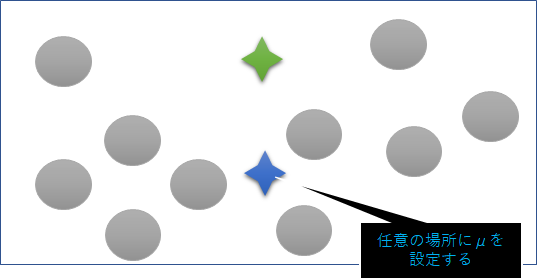
②クラス指示変数の更新
それぞれのデータプロットを最短距離となるμのクラスターにクラスタリングする。
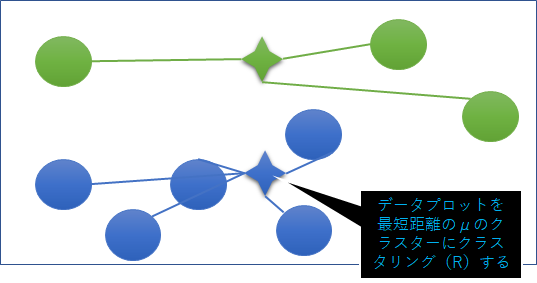
③中心ベクトルの更新
μの位置を当該クラスターのデータプロットの重心に更新する。
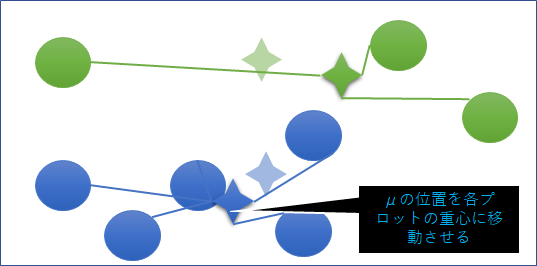
④再度クラス指示変数の更新
新たなμの位置からデータプロットを最短距離によりクラスタリングを再度実施する。
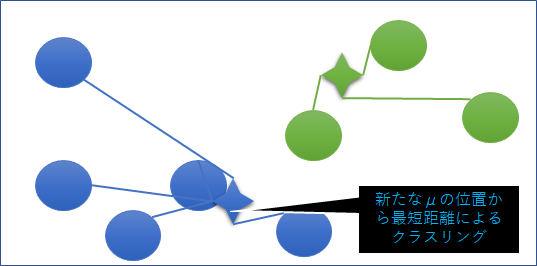
⑤相互更新の繰り返し
以降、μの位置が変わらなくなるか任意の回数だけ相互更新を繰り返す。
なんとなく数値的に近いものでうまくクラスタリングされそうな気がしてきますね。
K-means法の理論
以下、上記のイメージに沿って数式を使った内容を確認していきたいと思います。
①初期値の設定
データプロット上に任意のクラスター中心ベクトルμを設定する。
■中心ベクトルの設定
中心ベクトル(μ)はクラスターの数だけ設定するので、以下のように表現することができます。
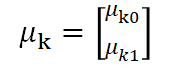
実際に数字を入れると以下のような感じです。

■クラス指示変数の設定
図中には表現されていませんが、数式上ではクラス指示変数(R)にも初期値を設定しておく必要があります。
各プロットがnで表現されるとき、3クラスターに対するクラス指示変数はベクトルを用いて以下のように表現することができます。
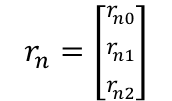
例えば5番目のプロットがクラス0に分類される場合には以下のように表現されます。
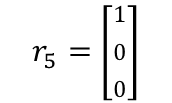
初期値としては全てのプロットはクラス0に分類させておくこととします。
また、全てのプロットをまとめると以下の表現することができます。
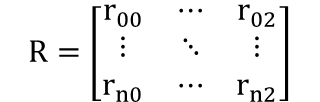
■入力データの設定
入力プロットデータは対象とするデータセットによって入力されているものですが、数式上は以下のように表現することとします。
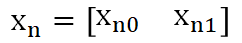
②クラス指示変数の更新
それぞれのデータプロットを最短距離となるμのクラスターにクラスタリングする。
ここではデータプロットとクラスターの中心ベクトルとの距離を測ることにより、指示変数の更新を行います。
今回のケースでは二次元グラフで考えているためこれはイメージしやすく、各プロットと各中心ベクトルとの絶対値をとり比較を行い最も値が小さいものにクラス指示変数を更新します。
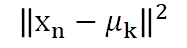
以下のようなイメージになります。
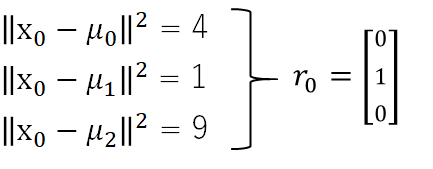
③中心ベクトルの更新
μの位置を当該クラスターのデータプロットの重心に更新する。
次にクラスターの中心ベクトルμを更新します。
中心ベクトルμはクラスターに所属する各プロットの重心となるので、プロットの座標平均を以下の表現します。
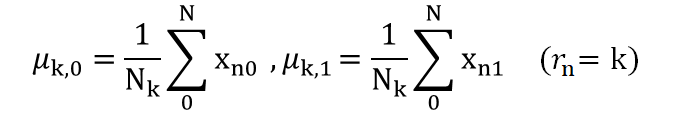
上記は0~Nまでのプロットxの中のクラスターkに所属するもののみを平均することを表しています。
数式上の表現として正しいのかはちょっと微妙です。
これを今回は3クラスターなので、k=0-2まで算出します。
④再度クラス指示変数の更新
新たなμの位置からデータプロットを最短距離によりクラスタリングを再度実施する。
あとは基本的に繰り返しで、「②クラス指示変数の更新」と同様に中心ベクトルとデータプロットの絶対距離を算出し、最短距離であるクラスターにクラス指示変数を更新していきます。
⑤相互更新の繰り返し
以降、μの位置が変わらなくなるか任意の回数だけ相互更新を繰り返す。
次はPythonで実装を行います。
記事を書き途中から久しぶりに書いたので、もしかしたら内容とか粒度が変な感じになってるかもしれないけどとりあえず更新。