ちょっと時間が空いてしまいましたが、今回はPythonで三次元グラフを扱います。
三次元グラフ
三次元の数式
これまで、Python学習においてはもちろん、学生時代の数学でも三次元のグラフというのはあまり扱ってきませんでした。
二次元というのはx軸とy軸を持つグラフでしたので、三次元ではx軸、y軸、z軸の三方向性を持つグラフとなります。
数式で表してみると例えば以下のようなものになります。
z = x + 2y
Pythonで表現してみます。
・例
# ライブラリのインポート
import numpy as npy
# 関数の定義
def f(x,y):
return x + 2*y
linelen = 3
# X軸とY軸に-5から5までの配列
xline = npy.linspace(0,2,linelen)
yline = npy.linspace(0,2,linelen)
# Z軸に0、0の要素を必要な数だけ用意する
zline = npy.zeros((len(xline),len(yline)))
# X軸のループ
for i0 in range(linelen):
# Y軸のループ
for i1 in range(linelen):
zline[i1,i0] = f( xline[i0], yline[i1])
print(zline)・出力結果
[[0. 1. 2.] [2. 3. 4.] [4. 5. 6.]]
表現として正しいのか分かりませんが(x, y)としたとき以下に対応していることになるので出力結果が正しいのはわかるでしょう。
[[(0,0) (1,0) (2,0)]
[(0,1) (1,1) (2,1)]
[(0,2) (1,2) (2,2)]]
数値を色で表現する
三次元グラフの出力結果を色で表現してみます。
グラフ表現を行うので「matplotlib.pyplot」(plt)を使用します。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f(x,y):
return x + 2*y
linelen = 3
# X軸とY軸に0から2までの配列
xline = npy.linspace(0,2,linelen)
yline = npy.linspace(0,2,linelen)
# Z軸に0、0の要素を必要な数だけ用意する
zline = npy.zeros((len(xline),len(yline)))
# X軸のループ
for i0 in range(linelen):
# Y軸のループ
for i1 in range(linelen):
zline[i1,i0] = f( xline[i0], yline[i1])
# 数値を灰色階調で表現する
plt.gray()
# pltに要素を設定する
plt.pcolor(zline)
# 右側にカラーバーを表示する
plt.colorbar()
plt.show()
・出力結果

出力結果をみると一瞬???となりました。
行列表現と異なるように見えますが、左下から値を出力し始めるようなので以下のように結果が出力されており正しいことがわかります。
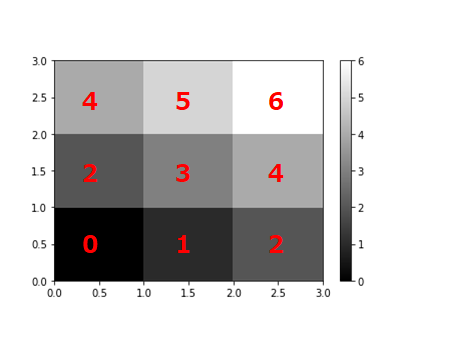
グレースケールのみでなく他の色での表現も可能なようです。すごいなぁ純粋に感心。
これで三次元関数を可視化することができました。
現時点ではだから何?って感じはしますがまぁ進めていきましょう。
数値を表面で表現する
色の表現で少しはそれっぽくなりましたが、表現方法としては二次元です。
実際に三次元で表現するのがここからの方法。
三次元の表現を行うためには以下のAxes3Dをインポートを行う必要があるようです。
from mpl_toolkits.mplot3d import Axes3D
正直いきなりやると何がなんだか分からなくなりますが、一つ一つ理解していくかまずは固定表現として覚えてしまうでよいのではないかと思います。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f(x,y):
return x + 2*y
linelen = 3
# X軸とY軸に0から2までの配列
xline = npy.linspace(0,2,linelen)
yline = npy.linspace(0,2,linelen)
# Z軸に0、0の要素を必要な数だけ用意する
zline = npy.zeros((len(xline),len(yline)))
# X軸のループ
for i0 in range(linelen):
# Y軸のループ
for i1 in range(linelen):
zline[i1,i0] = f( xline[i0], yline[i1])
# x軸とy軸を行列表現にする
xline, yline = npy.meshgrid(xline, yline)
# 座標系の指定
ax = plt.subplot( 1, 1, 1, projection ='3d')
# 表面の表示
ax.plot_surface( xline, yline, zline, rstride = 1, cstride = 1, alpha = 0.3, color ='blue', edgecolor ='black')
# Z軸の表示をずらす
ax.set_zticks(( 0, 0.2))
# グラフの向きを調整する
ax.view_init( 75, -95)
plt.show()・出力結果
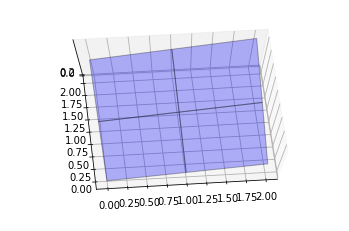
これだけ見てもいまいち正しいのかわからない気がします。自身が理解できる形にグラフを調整してみましょう。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f(x,y):
return 2*x*x - 2*y
linelen = 10
# X軸とY軸に0から5までの配列
xline = npy.linspace(0,5,linelen)
yline = npy.linspace(0,5,linelen)
# Z軸に0、0の要素を必要な数だけ用意する
zline = npy.zeros((len(xline),len(yline)))
# X軸のループ
for i0 in range(linelen):
# Y軸のループ
for i1 in range(linelen):
zline[i1,i0] = f( xline[i0], yline[i1])
# x軸とy軸を行列表現にする
xline, yline = npy.meshgrid(xline, yline)
# 座標系の指定
ax = plt.subplot( 1, 1, 1, projection ='3d')
# 表面の表示
ax.plot_surface( xline, yline, zline, rstride = 1, cstride = 1, alpha = 0.3, color ='blue', edgecolor ='black')
# Z軸の表示をずらす
ax.set_zticks((-10, 0, 40))
# グラフの向きを調整する
ax.view_init( 20, -100)
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
plt.show()・出力結果
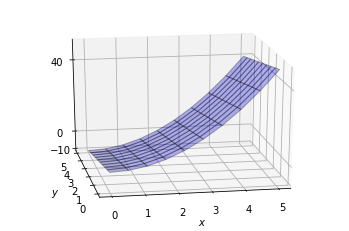
とりあえずで、ちゃかちゃかといじってみると何となく関数の使い方もわかってくるものです。
関数は少し変化を大きくするために以下のようにしてみました。
z = 2x^2 -2y
X軸とY軸の範囲を0から5までにする。スポットは10個。
linelen = 10 # X軸とY軸に0から5までの配列 xline = npy.linspace(0,5,linelen) yline = npy.linspace(0,5,linelen)
グラフの取りうる最大値や最小値から表示値を決めます。
# Z軸の表示をする ax.set_zticks((-10, 0, 40))
見やすいように調整したが、まだいまいちわからない。
# グラフの向きを調整する ax.view_init( 20, -100)
X軸とY軸を明示する。
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')単純な関数なのであまり面白くはないですが
x=5,y=0のとき最大値をとり
x=0,y=5のとき最小値をとるので思い通りのグラフになっていることがわかりました。
グラフの描写はこんなところまで、段々道具がそろってきた感じがしますね。
次回はちょっと数学に触れます。
サンプルソース
https://github.com/wantanblog/python_dev/blob/master/python_Graph3.ipynb