長くなってきたので一旦切りました。行列の続きです。
特殊な行列
数学的に特殊という言葉が適切なのか分かりませんが、主に行列の乗算において出現する名前がついている行列を少し紹介します。
正方行列
これは見た目でイメージがしやすいと思います。
行と列の数が同じ行列のことを指します。
行列の乗算においては、正方行列同士の乗算は要素数が変わらないという特徴をもちます。

・例
import numpy as npy
# 正方行列の乗算
# 行列の定義
A = npy.array([[2,0],[4,-2]])
B = npy.array([[3,5],[2,-3]])
result1 = A.dot(B)
result2 = B.dot(A)
print("A×Bの解")
print(result1)
print("B×Aの解")
print(result2)・出力結果
A×Bの解 [[ 6 10] [ 8 26]] B×Aの解 [[ 26 -10] [ -8 6]]
単位行列
数学における「単位〇〇」というのは、その分野の基準とできるような値、「1」を表すことが多いです。
行列においても、特に行列の乗算において、スカラーの「1」と同じ働きをするものを指しています。
つまりは、乗算後も乗算前と結果が変わらないということになります。
視覚的には正方行列で、斜めに1が並んだような形の以下のようなものを指します。

・例
import numpy as npy
# 単位行列の乗算
# 行列の定義
A = npy.array([[2,0],[4,-2]])
B = npy.array([[1,0],[0,1]])
result1 = A.dot(B)
result2 = B.dot(A)
print("A×Bの解")
print(result1)
print("B×Aの解")
print(result2)・出力結果
A×Bの解 [[ 2 0] [ 4 -2]] B×Aの解 [[ 2 0] [ 4 -2]]
逆行列
逆行列はある固有の行列を指すものではありません。
ある行列Aが存在するとき、行列の乗算を行った結果が単位行列になるものを、Aの逆行列と言います。

このとき行列Bは行列Aの逆行列ということができ一般には「A^-1」で表現されます。
これはスカラーの逆数表現と同じことです。

この逆行列の各要素を変数でおくことによって、行列の乗算から連立方程式により算出することも可能ですが、逆行列を求めるための公式が存在します。
【公式】

この公式、どこまで覚えておけばいいのかというのは分かりませんが、数学的な素養としては上記のような式をみたときに、逆行列が存在しない行列も存在するのだということは瞬時に察したいところです。
逆行列のスカラー部分の分母が「ad-bc」となっているので、これが「0」になるパターンは発散するため、逆行列を求めることができない。つまりは存在しないということになります。
Pythonではライブラリ「npy.linalg.inv」によって、逆行列を求めることができます。
2×2ならまでしも要素数が大きくなってくると、自力で求めることが困難になってくるのでこれは必須ですね。
・例
import numpy as npy
# 逆行列の算出
# 行列の定義
A = npy.array([[1,2],[3,4]])
B = npy.array([[3,2,-2],[2,5,6],[10,-5,2]])
C = npy.array([[1,2],[2,4]])
result1 = npy.linalg.inv(A)
result2 = npy.linalg.inv(B)
#result3 = npy.linalg.inv(C)
print("Aの逆行列")
print(result1)
print("Bの逆行列")
print(result2)
print("Cの逆行列")
#print(result3)・出力結果
Aの逆行列 [[-2. 1. ] [ 1.5 -0.5]] Bの逆行列 [[ 0.11363636 0.01704545 0.0625 ] [ 0.15909091 0.07386364 -0.0625 ] [-0.17045455 0.09943182 0.03125 ]] Cの逆行列
ちなみに逆行列が存在しない行列Cを「npy.linalg.inv」によって逆行列を算出しようとしたところ、「LinAlgError: Singular matrix」となりました。
実践的には必ず例外処理を行っておくべきところなのかもしれません。
また逆行列「ad-cd」の部分を行列式といい、以下のように表現されます。

その他の行列の操作と性質
転置
ベクトル回にもでてきた操作ですが、行列でも同じことができます。
操作としては行と列を入れ替えるイメージでよいでしょう。
数式上では「T」をつけて表現します。

Pythonの実装においても、ベクトルの操作と同様に行列に対する「.T」によって操作を行います。
・例
import numpy as npy
# 転置操作
# 行列の定義
A = npy.array([[2,4,1],[-6,2,11]])
AT = A.T
print("行列A")
print(A)
print("行列Aの転置")
print(AT)・出力結果
行列A [[ 2 4 1] [-6 2 11]] 行列Aの転置 [[ 2 -6] [ 4 2] [ 1 11]]
行列と連立方程式
高校数学でもやったような記憶が少しだけあります。
以下のような連立方程式を題材とします。

さすがに連立方程式の解き方は省略しますが、普通に解いて「x=3、y=-4」が求められます。
これを行列を利用して解いてみます。
まずは上記の連立方程式を行列を用いて表現します。

なぜこのような形で表現できるかというと、左辺を乗算した結果が以下になるためです。

しかし、そのまま展開してしまうと普通の連立方程式になってしまうので、行列で解くときは行列の性質を用いて解きます。

なにをやっているかと言うと、左辺の行列の逆行列を左から乗算することによって左辺の変数部分以外を単位行列とします。
単位行列は変数を含む行列に乗算しても結果は変わらずです。
つまりは、右辺側で逆行列を求めて、それを乗算することによって連立方程式の解を求めることができます。
よくできてますね。
右辺側の計算は面倒なので省略してしまいましたが、面倒なことはPythonに任せてみましょう。
・例
import numpy as npy
# 連立方程式を解く
# 行列の定義
left = npy.array([[2,-1],[3,2]])
right = npy.array([[10],[1]])
# 逆行列を求める
left_rev = npy.linalg.inv(left)
# 逆行列を乗算する
result = left_rev.dot(right)
print("逆行列")
print(left_rev)
print("連立方程式の解")
print(result)・出力結果
逆行列 [[ 0.28571429 0.14285714] [-0.42857143 0.28571429]] 連立方程式の解 [[ 3.] [-4.]]
見事求められていますね。
逆行列で小数(分数)になっている部分もPythonなら何の苦もなく算出することができます。
連立方程式の変数が2つならば普通に解いた方が早いですが、変数が増えてきたときに効果を発揮するとあります。
Pythonにより求めることができるならばなおさらですね。
例えば以下、自分で作ったので解は分かっていて「x=2、y=-1、z=-5」ですが、解くのはめんどくさくなってくるところではないでしょうか。

・例
import numpy as npy
# 連立方程式を解く
# 行列の定義
left = npy.array([[3,1,-1],[-2,4,-3],[7,3,2]])
right = npy.array([[10],[7],[1]])
# 逆行列を求める
left_rev = npy.linalg.inv(left)
# 逆行列を乗算する
result = left_rev.dot(right)
print("逆行列")
print(left_rev)
print("連立方程式の解")
print(result)・出力結果
逆行列 [[ 0.25 -0.07352941 0.01470588] [-0.25 0.19117647 0.16176471] [-0.5 -0.02941176 0.20588235]] 連立方程式の解 [[ 2.] [-1.] [-5.]]
今回はわざわざ複数行に分けて実行していますが、これが一行で算出できるのはすごいですね。
写像(変換)
これは私にとって新しい概念です。
ベクトルについては、比較的分かりやすく(矢印状で)図示することができましたが、行列についても同じく表現可能だそうです。
ベクトルに対する行列は「ベクトルを別なベクトルに変換する規則」と捉えることができます。
乗算操作などによって、元のベクトルを一定の規則で別のベクトルに変換できることから。
このようにベクトルなどのグループからグループへ対応関係を与える規則を写像(変換)(タイトル回収)と言います。
特に行列は線形写像(線形変換)と言われるそうです。
pythonを少しいじってみましょう。
(1,0)の点(ベクトル)を以下の行列にかけて写像してみます。

適切な表現が分からなかったのでかなり無理やりな表現になっています。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 行列を乗算する関数の定義
def f(x):
A = npy.array([[3,1],[-2,4]])
return A.dot(x)
#ベクトルの定義
vector = npy.array([[1],[0]])
vector2 = f(vector)
# FigureとAxesを描画
fig, ax = plt.subplots(figsize = (5, 5))
ax.grid()
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
plt.scatter(vector[0],vector[1])
plt.scatter(vector2[0],vector2[1])
# 指定した位置に注釈と矢印を入れる
ax.annotate("", xy = (vector2[0], vector2[1]), size = 15, xytext = (vector[0], vector[1]),
color = "red", arrowprops = dict())
# グラフを描写する
plt.show()・出力結果

少し試してみましょう。
xとyがそれぞれ-2~2まで範囲の点(ベクトル)、つまりは25個のベクトルに対する写像を表現してみます。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 行列を乗算する関数の定義
def f(x):
A = npy.array([[3,1],[-2,4]])
return A.dot(x)
xlist = npy.arange(3)
ylist = npy.arange(3)
xlist = [-2,-1,0,1,2]
ylist = [-2,-1,0,1,2]
# FigureとAxesを描画
fig, ax = plt.subplots(figsize = (5, 5))
ax.grid()
ax.set_xlim(-15, 15)
ax.set_ylim(-15, 15)
for xi in xlist :
for yi in ylist:
#ベクトルの定義
vector = npy.array([[xi],[yi]])
vector2 = f(vector)
plt.scatter(vector[0],vector[1])
plt.scatter(vector2[0],vector2[1])
# 指定した位置に注釈と矢印を入れる
ax.annotate("", xy = (vector2[0], vector2[1]), size = 5, xytext = (vector[0], vector[1]),
color = "red", arrowprops = dict())
# グラフを描写する
plt.show()・出力結果
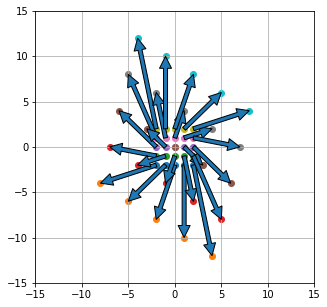
図的には少し見にくくなってしまいましたが、これによりベクトルに対して行列を乗算する(写像)ことによって、一定の規則に基づいてベクトルの変換が行われていることが図として確認できると思います。
これはニュートラルネットワークに使用されるそうで、入力要素xと出力結果yをベクトルと見なし、重みWを行列と見なしたとき、
入力結果(x)×重み(W)=出力結果(y)
と表現され、これはそのまま、線形写像ということができます。
固有ベクトル
端折り気味にいきます・・
正方行列Aに対して、次の式を満たす列ベクトルが存在するとき、λ(ラムダ)を固有値、xを固有ベクトルと言います。
※Eは単位行列
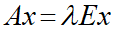
このとき、以下のように式を変形でき、逆行列が存在するとき「x=0」となるため、固有ベクトルを持たないということになります。
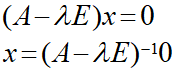
つまり、行列式が0となる以下の条件を満たしたときに固有ベクトルが存在すると言い換えることができます。

固有ベクトルを実際に求めてみます。
まずは行列式を用いて、固有値λから求めます。
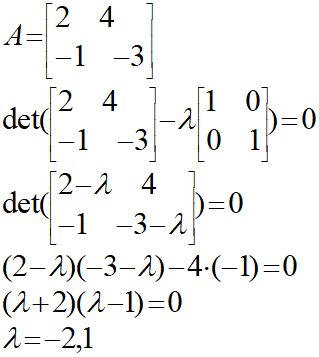
この固有値に対して、それぞれ固有ベクトルxを求める流れとなります。

固有ベクトルをx=(α、β)とすると以下のように進められます。

この結果より、固有ベクトルは(1、-1)の定数倍と求めることができました。
疲れた。
同様に「λ=1」の場合も求めると、(4、-1)の定数倍と求めることができます。
なんで無理やり紹介したかと言うと、これが教師なし学習における主成分分析等に使われると聞いたからです。
Pythonでなんか実装しようとしたけど、今の自分の理解ではすぐにはできませんでした・・・
・今回のソース(前回の続き)
python_dev/Python_math4.ipynb at master · wantanblog/python_dev · GitHub