またまたしばらくサボっていました。
今回は指数対数ということで、機械学習を勉強しようと思ったことがある人はみたことがあるであろうシグモイド関数などがでてきます。
概要はつかんでおきたいですね。
個別の関数については難しくてギブアップ気味・・
指数関数と対数関数の基本
指数と対数を個別にまとめようかと思いましたが、微分が入ってくることを考えると指数と対数はきってもきれない関係になるのでまとめてご紹介します。
指数関数ってなんだっけ?
指数自体はこれまでの関連記事でも普通につかってきましたし、まぁだいたいの人は知っているでしょう。
以下のようにその数を何回乗算するかというものになります。
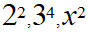
指数表現では、右肩部分を指数それに対して普通の数字部分を底と呼びます。
そこで、指数関数とはなにかというと、底を定数として指数部分を変数とした関数になります。

指数関数と言えば、指数関数的に増加していくなどの表現が使用されることもありますが、実際のグラフで表現しておきましょう。
Pythonを使います。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f1(x):
return 2**x
def f2(x):
return -2**x
# X軸に0から9までの配列
xline = npy.linspace(-3,6,50)
yline1 = f1(xline)
yline2 = f2(xline)
# pltに要素を設定する
plt.plot(xline, yline1, color ='black', label='$func1$')
plt.plot(xline, yline2, color ='blue', label='$func2$')
# 凡例を表示する
plt.legend(loc="upper left")
# y軸の表示範囲を設定する
plt. ylim(- 50, 50)
# y軸の表示範囲を設定する
plt. xlim(- 2, 5)
# タイトルを表示する
plt.title('$SampleGraph$')
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
# グリッドを表示する
plt.grid(True)
# グラフを描写する
plt.show()・出力結果
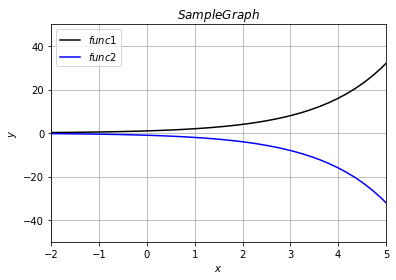
関数1が底が正の数の場合の関数の形で、xがマイナスの極限でyが0になり、xがプラスの極限でyが無限大になる。
底が負の数の場合、xがマイナスの極限でyが0になり、xがプラスの極限でyがマイナスの無限大になると。
この辺はまぁ大丈夫ですかね。
対数関数ってなんだっけ?
対数に初めて出くわすのが数学ではいつだったかあまり覚えていませんが、いわゆるlogのことですね。
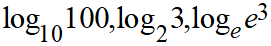
対数表現では、logの右下部分の数字を底、その後に続く数字部分を真数と呼びます。
対数というのはなかなか言葉での表現が難しいですが普通の数字で表現しようとすると以下のようになります。
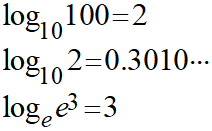
数学で対数をどのように説明されたかあまり覚えていませんが、真数が底の何乗になっているかと考えればよいでしょう。
よく出現する対数には名前がついていおり、底が10の対数を常用対数、底がeの対数を自然対数と呼びます。
自然対数の底に使用されるeはネイピア数と呼ばれ、値としては2.71828…となります。
前置きが長くなりましたが、対数関数とは底が定数で、真数が変数となっている関数のことです。
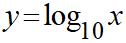
対数関数もPythonで表現してみます。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f1(x):
return npy.log10(x)
# X軸に0から9までの配列
xline = npy.linspace(0,21,500)
yline1 = f1(xline)
# pltに要素を設定する
plt.plot(xline, yline1, color ='black', label='$func1$')
# 凡例を表示する
plt.legend(loc="upper left")
# y軸の表示範囲を設定する
plt. ylim(- 2, 2)
# y軸の表示範囲を設定する
plt. xlim(- 1, 20)
# タイトルを表示する
plt.title('$SampleGraph$')
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
# グリッドを表示する
plt.grid(True)
# グラフを描写する
plt.show()・出力結果
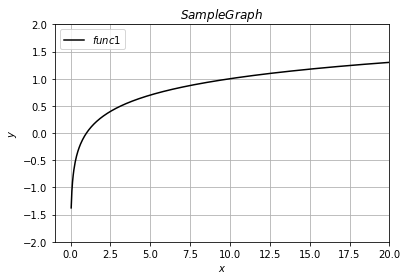
Python上での注意点は0付近がうまく表現しにくいことでしょうか。
上記では暫定的にプロット数を増やして表現しています。
対数関数は指数関数の逆関数と言われることがあります。
指数関数の微分
指数関数の微分は以下の公式により表現されます。
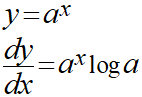
ここでのlogは自然対数となるので、以下のことがわかります。
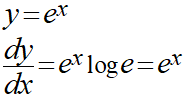
底がe(ネイピア数)の指数関数を微分すると微分前後で結果が変わらないということです。
微分の定義から求めることも可能ですが、ここではPythonでの微分前後のグラフを表現してみます。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f1(x):
return 2**x
def f2(x):
return 2**x*npy.log(2)
# X軸に0から9までの配列
xline = npy.linspace(-3,6,50)
yline1 = f1(xline)
yline2 = f2(xline)
# pltに要素を設定する
plt.plot(xline, yline1, color ='black', label='$func1$')
plt.plot(xline, yline2, color ='blue', label='$func2$')
# 凡例を表示する
plt.legend(loc="upper left")
# y軸の表示範囲を設定する
plt. ylim(- 5, 50)
# y軸の表示範囲を設定する
plt. xlim(- 2, 5)
# タイトルを表示する
plt.title('$SampleGraph$')
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
# グリッドを表示する
plt.grid(True)
# グラフを描写する
plt.show()・出力結果

関数2が関数1の微分結果を表しています。
対数関数の微分
対数関数の微分公式は以下のようになります。
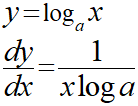
対数の微分についても底がネイピア数の場合は、特殊なケースと捉えることができます。
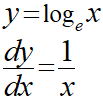
どちらかというと底がeであるこちらの公式の方がよく出てくるみたいですね。
こちらもPythonで、微分前後の結果をグラフを表現してみましょう。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f1(x):
return npy.log(x)
# 関数の定義
def f2(x):
return 1/x
# X軸に0から9までの配列
xline = npy.linspace(0.000001,21,500)
yline1 = f1(xline)
yline2 = f2(xline)
# pltに要素を設定する
plt.plot(xline, yline1, color ='black', label='$func1$')
plt.plot(xline, yline2, color ='blue', label='$func2$')
# 凡例を表示する
plt.legend(loc="upper left")
# y軸の表示範囲を設定する
plt. ylim(- 2, 4)
# y軸の表示範囲を設定する
plt. xlim(- 1, 20)
# タイトルを表示する
plt.title('$SampleGraph$')
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
# グリッドを表示する
plt.grid(True)
# グラフを描写する
plt.show()・出力結果
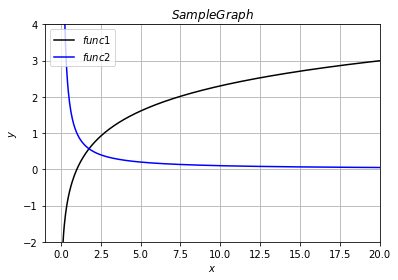
関数1が微分前、関数2が微分後の反比例の関数を表しています。
特殊な関数
特殊なというよりは名前がついている関数でしょうか。
シグモイド関数
シグモイド関数というのは以下のような関数のことを指します。
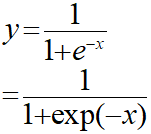
ネイピア数の指数関数はexp(x)の形で表現できるので、2行目のような式で表現することも可能です。
シグモイド関数なんてきいたことない?私も機械学習にふれようとするまでは知らなかったのでたぶん大丈夫です。
まずはさっそくPythonでどのようなグラフになるのか表現してみましょう。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f1(x):
return 1/(1+npy.exp(-x))
# X軸に0から9までの配列
xline = npy.linspace(-21,21,500)
yline1 = f1(xline)
# pltに要素を設定する
plt.plot(xline, yline1, color ='black', label='$func1$')
# 凡例を表示する
plt.legend(loc="upper left")
# y軸の表示範囲を設定する
plt. ylim(- 2, 4)
# y軸の表示範囲を設定する
plt. xlim(-20, 20)
# タイトルを表示する
plt.title('$SampleGraph$')
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
# グリッドを表示する
plt.grid(True)
# グラフを描写する
plt.show()・出力結果
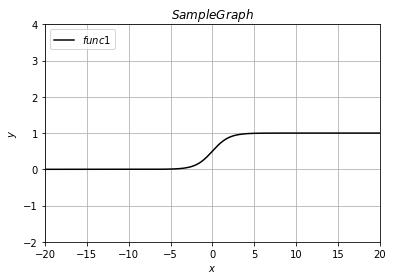
グラフの形を確認すると分かりますがシグモイド関数はxの値がマイナスの無限大からプラスの無限大までで、yが0から1までの値をとることが分かります。
この特徴からシグモイド関数は、確率を表現する場合やニュートラルネットワークなどの人工知能モデルの表現力を高めるために使用されるようです。
ソフトマックス関数
一体なんだ??
ソフトマックス関数とは複数の出力結果を、その大小関係を保ったままそれぞれを確率で表現するための関数のことです。
※ただしいかな??
確率で表すとはつまり、全ての事象(出力結果)を総和すると1.0(100%)で表現するということです。
以下の3つの数値で考えてみます。
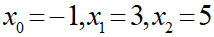
このとき元の値のexpを求めます。
expのとりうる範囲は0以上となるので、マイナス値が入っていても正の数の範囲で値を大きさとして表現することが可能となるのです。
ソフトマックス関数の公式は以下の通り(要素3つの場合)です。
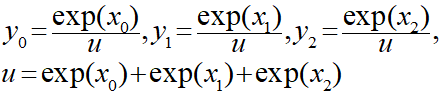
それぞれの値は分母に3つの合計となるuとすることで合計が1となるようにします。
手計算で求めるのはしんどいのでPythonで求めましょう。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f1(x0,x1,x2):
u = npy.exp(x0)+npy.exp(x1)+npy.exp(x2)
return npy.exp(x0)/u, npy.exp(x1)/u, npy.exp(x2)/u
x0=-1
x1=3
x2=5
result = f1(x0,x1,x2)
print("元データ")
print(x0,x1,x2)
print("生データ")
print(result)
print("整形")
print(npy.round(result,3))
print("合計")
print(npy.sum(result))
・出力結果
元データ -1 3 5 生データ (0.0021785213571970234, 0.11894323591065209, 0.878878242732151) 整形 [0.002 0.119 0.879] 合計 1.0
【シグモイド関数とソフトマックス関数】
詳細は省きますがシグモイド関数とソフトマックス関数は微分すると以下のような形になります。
・シグモイド関数の微分
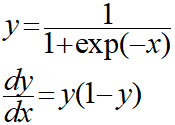
・ソフトマックス関数の微分
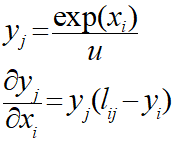
細かいところは私も理解しきれませんでした。
微分後の式の形が同形になっていることがわかります。
これはシグモイド関数とソフトマックス関数自体が根本的に同じ形であることからきています。
2つの要素に対するソフトマックス関数を考えます。
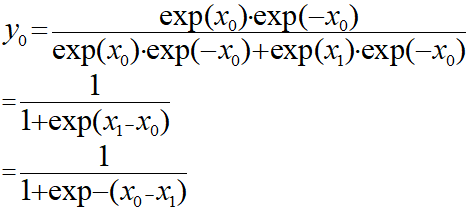
公式の分子分母にexp(x0)を乗算することにより式を整理すると上記のようになります。
つまりは変数を(x0-x1)としたシグモイド関数ということができます。
式の意味からとらえると、シグモイド関数は特定の値を0~1の範囲に値を変換するものなので、ソフトマックス関数はシグモイド関数を多変数に拡張した概念と捉えることができます。
ガウス関数
ガウス関数は以下のような式で表されます。
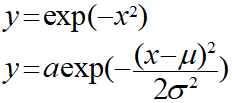
Pythonでグラフの形を確認してみます。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# 関数の定義
def f1(x):
return npy.exp(-x**2)
def f2(x):
return 0.5*npy.exp(-(x-1)**2/(2*3**2))
# X軸に0から9までの配列
xline = npy.linspace(-8,8,50)
yline1 = f1(xline)
yline2 = f2(xline)
# pltに要素を設定する
plt.plot(xline, yline1, color ='black', label='$func1$')
plt.plot(xline, yline2, color ='blue', label='$func2$')
# 凡例を表示する
plt.legend(loc="upper left")
# y軸の表示範囲を設定する
plt. ylim(- 0.1, 1.2)
# y軸の表示範囲を設定する
plt. xlim(-7, 7)
# タイトルを表示する
plt.title('$SampleGraph$')
# X軸に名前を付ける
plt.xlabel('$x$')
# Y軸に名前を付ける
plt.ylabel('$y$')
# グリッドを表示する
plt.grid(True)
# グラフを描写する
plt.show()・出力結果
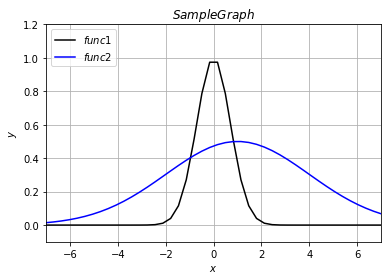
グラフの形を見るとなんとなく想像がつくかもしれませんが、正規分布を表す関数になります。
つまりは確率の分布です。
μが平均、σが標準偏差を表し、aでグラフの高さを調整します。
【二次元のガウス関数】
ガウス関数は入力をベクトルなどに置き換え、二次元に拡張して用いられることがあります。
グラフ上では三次元になるということです。
入力を二次元ベクトルとした場合は以下のようになります。
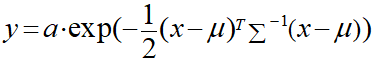
グラフの形はμとΣのパラメータによって定まります。
μは中心ベクトルと言われるもので、グラフの中心を表します。
Σは共分散行列と言われるもので、2×2の正方行列です。
・例
# ライブラリのインポート
import numpy as npy
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Jupiter Notebookで結果を表示するためのおまじない
%matplotlib inline
# ガウス関数の定義
def f1(x,mu,sigma):
N,D = x.shape
c1 = 1/(2*npy.pi)**(D/2)
c2 = 1/(npy.linalg.det(sigma)**(1/2))
inv_sigma = npy.linalg.inv(sigma)
c3 = x - mu
c4 = npy.dot(c3, inv_sigma)
c5 = npy.zeros(N)
for num in range(D):
c5 = c5 + c4[:,num]*c3[:,num]
p = c1 * c2 * npy.exp(-c5/2)
return p
X_range0 = [-3,3]
X_range1 = [-3,3]
# 高等線の表示
def show_contour_gauss(mu,sigma):
xnum = 40
x0 = npy.linspace(X_range0[0],X_range0[1],xnum)
x1 = npy.linspace(X_range1[0],X_range1[1],xnum)
xx0, xx1 = npy.meshgrid(x0, x1)
x = npy.c_[npy.reshape(xx0, xnum * xnum, 1), npy.reshape(xx1, xnum * xnum, 1)]
f = f1(x, mu, sigma)
f = f.reshape(xnum,xnum)
f = f.T
cont = plt.contour(xx0,xx1,f,15,colors='K')
plt.grid(True)
# 3D表示
def show3d_gauss(ax, mu, sigma):
xnum = 40
x0 = npy.linspace(X_range0[0],X_range0[1],xnum)
x1 = npy.linspace(X_range1[0],X_range1[1],xnum)
xx0, xx1 = npy.meshgrid(x0, x1)
x = npy.c_[npy.reshape(xx0, xnum * xnum, 1), npy.reshape(xx1, xnum * xnum, 1)]
f = f1(x, mu, sigma)
f = f.reshape(xnum,xnum)
f = f.T
ax.plot_surface(xx0,xx1,f,rstride=1,cstride=1,alpha=0.3,color='blue',edgecolor='black')
mu = npy.array([0.2,0.3])
sigma = npy.array([[2,-1],[1,1]])
Fig = plt.figure(1,figsize=(7,3))
Fig.add_subplot(1,2,1)
show_contour_gauss(mu,sigma)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.xlabel('$x_0$',fontsize=14)
plt.ylabel('$x_1$',fontsize=14)
Ax = Fig.add_subplot(1,2,2, projection='3d')
show3d_gauss(Ax, mu, sigma)
Ax.set_xlabel('$x_0$',fontsize=14)
Ax.set_ylabel('$x_1$',fontsize=14)
Ax.set_zticks([0.05,0.10])
Ax.view_init(20,-100)
plt.show()・出力結果
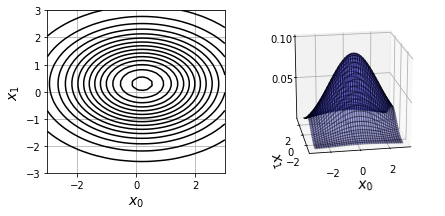
うーん難しい。
あんまりやりたくなかったけど妥協して次に進みますか・・
・今回のソース(前回の続き)
python_dev/Python_math5.ipynb at master · wantanblog/python_dev · GitHub