線形回帰モデルではこれまで最も基本的な一次元入力と二次元入力を扱ってみましたが、今回は多次元(N次元)線形回帰モデルを扱います。
入力の次元数を限定しないことによって、本格的な活用も可能になってくるかと思います。
煩雑になってくるかもしれませんが、一つの区切りとなるので頑張ります。
N次元線形回帰モデル
N次元線形回帰モデル(重回帰分析)
少し数学的な話が続くので辛い。
最初は入力パラメータが1次元で直線モデル、次に二次元になって面モデル、次元が増えたときにモデル自体が命名されているのかは分かりませんが、これは全て線形回帰モデルです。
・直線モデル
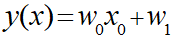
・面モデル
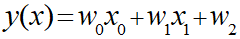
これらから線形回帰モデルはN次元で一般化して以下のように表現することが可能です。
このように入力パラメータがNになる回帰分析のことを重回帰分析と呼ぶらしいです。
・線形回帰モデル
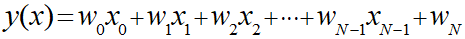
モデルのパラメータ解析解(単純化モデル)
解析解とは数学的に導出した解(w)のことです。
N次元モデルの解析解について考えていきますが、まずは単純化して線形モデルの切片を排除して考えていきます。
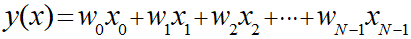
このとき、行列表記を用いるとこのモデルは以下のように表現することができます。
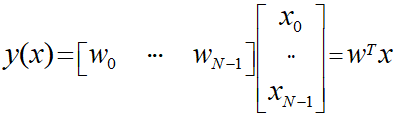
ここから実際に平均二乗誤差Jを導出していきます。
平均二乗誤差は今まで通り以下の式を使用します。
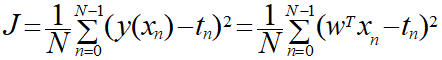
これまでと同様にwの解を求めるには偏微分を行います。
次元が低かった場合は実際にw0やw1の偏微分を求めることができましたが、N次元の場合は一つ一つ求めることができませんので一般化して求めます。
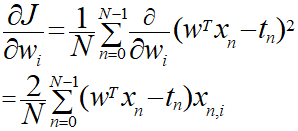
平均二乗誤差Jが最小になる値を求めるには、偏微分の結果がゼロになる場合の連立方程式を解くのでした。
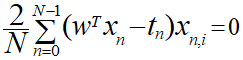
しかし、このままでは導出が困難なので、行列(ベクトル)を用いて導出します。
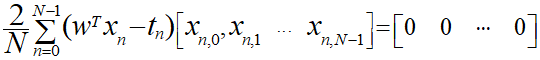
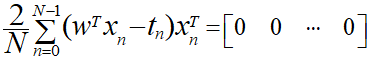
飛ばし気味になりますが、この式を展開します。
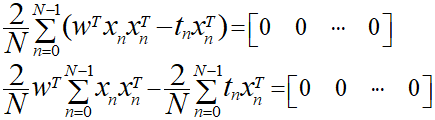
ここで、さらに単純化するために係数となる2/Nを排除するためにN/2を両辺に乗算し、行列式で置換します。
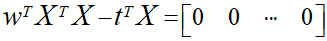
行列やベクトルなどを急にだしたので、少し整理しておきます。
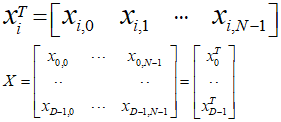
先に示した行列式の中身は上記の式の通りとなっています。
ここからwを求めるための式を導出していきます。
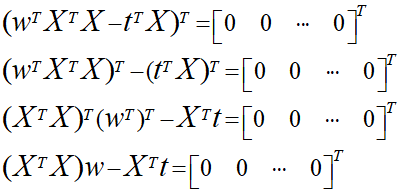
wの項以外を右側に移行し、逆行列を左から乗算することによってwを求めることができます。
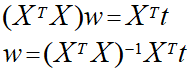
このwの式は入力パラメータとなるxが何次元であっても適用できます。
ちなみに右辺の式には「ムーア・ペンローズの擬似逆行列」という名前がついているらしいです。
モデルのパラメータ解析解
今導出したwの式は単純化した式だったので、次に正式な式で導出を行います。
正式な式とは単純化するために取り去った切片を付けた状態のことです。
線形回帰モデルは元々以下のような式でした。
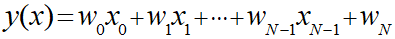
ここで切片の項にxを加えることで行列として考えられるように拡張します。
このときのxは「1」とすることで元の式と同様の式とみなすことができます。
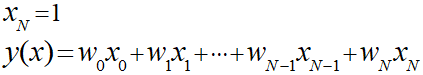
この式を用いると平均二乗誤差を求めるときに「N-1」までではなく「N」までの和を求めるようにして同様の導出を行うことで再現できます。

Pythonライブラリを用いた重回帰分析
だいぶ苦しくなってきたのでPythonライブラリを実装で濁します。
以下を参考にさせていただきました。
scikit-learn で線形回帰 (単回帰分析・重回帰分析) – Python でデータサイエンス
scikit-learnライブラリを用いた単回帰分析
今回はscikit-learnライブラリを用いますが
まずは使用方法を確認するために単回帰分析を行います。
データは下記記事で用いた単純なXとYの分析になります。
・例
# sklearn.linear_model.LinearRegression クラスを読み込み
from sklearn import linear_model
import pandas as pd
import numpy as npy
import matplotlib.pyplot as plt
clf = linear_model.LinearRegression()
# データをblog_data.npzファイルから取り出す
sample_data = npy.load('blog_data.npz')
X = sample_data['X']
X = npy.array([X]).T
Y = sample_data['Y']
# 予測モデルを作成
clf.fit(X, Y)
# 回帰係数
print(clf.coef_)
# 切片 (誤差)
print(clf.intercept_)
# 決定係数
print(clf.score(X, Y))
# 散布図
plt.scatter(X, Y)
# 回帰直線
plt.plot(X, clf.predict(X))・出力結果
[0.61743692] -130.73081352003646 0.9831086573905393
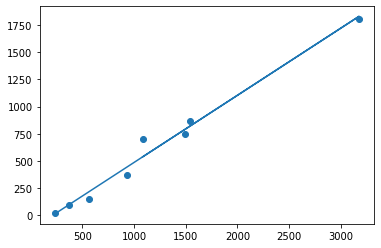
以前、ライブラリを用いた導出と同様の結果になりました。
重回帰分析
ここでやっと本題に入ります。
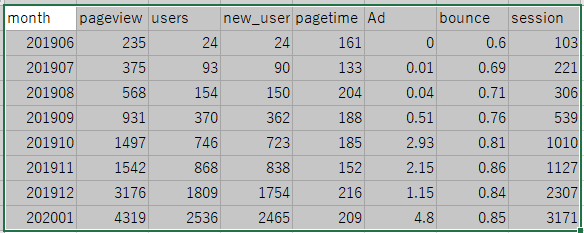
データは毎度おなじみのGoogleアナリティクスからとってきたブログに関連するデータを使用します。
今回は以下のような複数のパラメータをCSV形式で用意してある値に関する他のパラメータの相関を見ていきます。
・例
# sklearn.linear_model.LinearRegression クラスを読み込み
from sklearn import linear_model
clf = linear_model.LinearRegression()
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
blogdata = pd.read_csv("monthly_repo.csv", sep=",")
# 対象外の項目を除く
except_values = blogdata.drop("Ad", axis=1).drop("month", axis=1)
X = wine_except_quality.as_matrix()
Y = blogdata['Ad'].as_matrix()
# 予測モデルを作成
clf.fit(X, Y)
# 偏回帰係数
print(pd.DataFrame({"Name":except_values.columns,"Coefficients":clf.coef_}))
# 切片 (誤差)
print(clf.intercept_)・出力結果
Name Coefficients 0 pageview -0.004414 1 users -0.225594 2 new_user 0.249534 3 pagetime -0.007337 4 bounce 11.436902 5 session -0.007255 -4.730505205297209
こいつらがなにを表しているのか考えることが重要です。
今算出された値が重みwです。なので以下の式の各wに上記で算出した値を当てはめることで、本ブログに関する線形回帰モデルが生成できたことになります。
ちなみに各xはパラメータで、最後のWnが切片です。
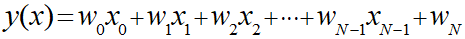
最後にリンク先の記事をまねて各パラメータの結果への影響度を測っておきたいと思います。
・例
# sklearn.linear_model.LinearRegression クラスを読み込み
from sklearn import linear_model
clf = linear_model.LinearRegression()
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
blogdata = pd.read_csv("monthly_repo.csv", sep=",")
# データフレームの各列を正規化
blogdata2 = blogdata.apply(lambda x: (x - np.mean(x)) / (np.max(x) - np.min(x)))
# 対象外の項目を除く
except_values = blogdata2.drop("Ad", axis=1).drop("month", axis=1)
X = except_values.as_matrix()
Y = blogdata2['Ad'].as_matrix()
# 予測モデルを作成
clf.fit(X, Y)
# 相関値
print(pd.DataFrame({"Name":except_values.columns,"Coefficients":npy.abs(clf.coef_)}))
# 切片 (誤差)
print(clf.intercept_)・出力結果
Name Coefficients 0 pageview 3.755232 1 users 118.060812 2 new_user 126.898203 3 pagetime 0.126866 4 bounce 0.619499 5 session 4.637096 -3.610323004487209e-15
本ブログの場合はユーザ数、新規ユーザ数が大きく影響を及ぼしているようです。
なんとなくは分かるけど、それならページビュー数とかセッション数も高くなりそうなものだけどなんでそうはならないんだろうか?
その辺は今後探れるようになれたらと思います。
・今回のソース
python_dev/Supervised_learning4.ipynb at master · wantanblog/python_dev · GitHub