前回までの
前回の記事では、MNISTという手書き文字画像データセットに対して、Kerasライブラリを活用してニューラルネットワークを実装し手書き文字の識別を行いました。
分類結果としては以下の通りで、正答率は「0.894」程度となりました。
今回は前回の実装に手を加えていくことで精度の向上を目指します。
なので、実装したモデルに対して精度を上げるための検討を行う練習となります。
なので、前回記事をベースにしているので足りない部分はそちらも参照を推奨。
活性化関数の検討
ReLu活性化関数
前回のニューラルネットワークで活性化関数としてシグモイド関数を使用しました。
久しぶりやることもあるので、活性化関数について少し確認しておきます。
・活性化関数
活性化関数(かっせいかかんすう、英: activation function)もしくは伝達関数(でんたつかんすう、英: transfer function)とは、ニューラルネットワークのニューロンにおける、入力のなんらかの合計(しばしば、線形な重み付け総和)から、出力を決定するための関数で、非線形な関数とすることが多い。

初学者だとこの必要性がなかなか理解しにくいように感じます。
以下のサイトが比較的分かりやすかったと思います。
活性化関数の役割と種類についてわかりやすく解説 | AVILEN AI Trend
・シグモイド関数とReLU関数の比較
前回活用したシグモイド関数と、今回適用するReLU関数の概形を確認しておきます。
シグモイド関数

ReLU関数

ReLU関数は以下の式で表現される関数です。

ReLU関数はシグモイド関数と比較して何が優れているのでしょうか?
そもそもこれまで使用していたシグモイド関数は特に多層のニューラルネットワークモデルの活性化関数として適用する場合、勾配消失が起きるため、適切に勾配を更新し続けられないという問題が発生しやすいと言われています。
勾配消失問題
現時点での私の理解でざっくりと行きます。
先に概要を述べるなら、パラメータ更新に活性化関数の偏微分式を含む逆伝播法では、ディープラーニングによる層の多層化によって初期層ほど活性化関数の偏微分式が掛けられた状態になります。
活性化関数にシグモイド関数を選択している場合、シグモイド関数の微分式は以下のグラフに示す通り、最大値が0.25であり、ニューラルネットワークの層が多層になるほどパラメータの更新量にこの値が乗算されていき極小化していくため、更新が起こらないあるいは適切な底に落ち着くまでに非常に時間がかかる。
とのことでした。

いくつかのサイトを参考にしましたのでそちらを参照した方が分かりやすいかもしれません。
勾配消失問題とは?
ニューラルネットワークの基礎 — ディープラーニング入門:Chainer チュートリアル
単純化した誤差逆伝搬法における3層ニューラルネットワーク(中間層は2層)を考えます。

入力値xを用いて、最終的な出力値yは以下のように表すことができます。

ここまで自体は特に問題ありません。
問題はこの次、重みの更新を行うところにあります。
式が見にくくなるので、活性化関数を通した出力値をHとします。
まず、各重みの更新については以下のように表現されるのでした。

出力層の重みw2の更新に使用される勾配ベクトルは以下のように表現されます。

同じく、中間層2の重みw1の勾配ベクトルはこう。

この辺は導出は以前の内容も参考にしていますので、詳細はそちらも参照。
www.wantanblog.com
まず着目すべきは∂H2/∂a2の部分です。
式中のHは活性化関数の出力値としておいているのでそれを戻すことで以下のように表現できることになります。

つまりは活性化関数h2の偏微分です。
最後に、中間層1の重みw0の勾配ベクトルについても確認しておきます。

この勾配ベクトルを展開した式の中に、活性化関数h2の偏微分式、活性化関数h1の偏微分式が含まれているのが分かります。
このことから逆伝播法のニューラルネットワークモデルでは層の初期段階ほど、それ以降の層の活性化関数の偏微分式がパラメータの更新量に乗算されていくということがわかります。
この問題に対応すべく、現在一般的に幅広く活性化関数に使用されているのがReLU関数というわけです。
これまで適用してきたシグモイド関数は偏微分式が1以下の値をとるのに対して、ReLU関数の微分式は以下のようになります。
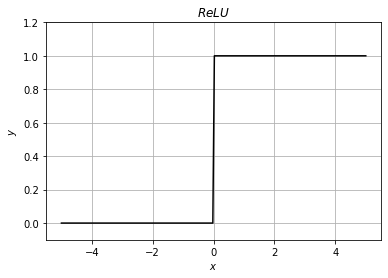
この通り正の数である限りは微分式として1を返し続けるので、シグモイド関数で起きていたような極端な更新量の減少は起こらなくなります。
KerasにおけるReLU関数の適用
実装
既にシグモイド関数を使用したニューラルネットワークを実装済みである場合、活性化関数にReLU関数を適用するのは非常に簡単です。
前回記事より「# ニューラルネットワークモデルの定義」部分のみ抜粋しております。
# ニューラルネットワークモデルの定義 from keras.models import Sequential from keras.layers import Dense, Activation from keras.optimizers import Adam npy.random.seed model=Sequential() # ReLu関数の適用 model.add(Dense(16,input_dim=784,activation='relu')) model.add(Dense(10,activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer=Adam(),metrics=['accuracy'])
activationに'relu'を設定するだけです。
もし他のコード部分が必要な場合は前回記事も参照ください。
結果の比較
活性化関数にシグモイド関数とReLU関数を適用した場合の出力結果を比較していきます。
■最終正答率
・シグモイド関数
TEST loss: 0.4908383786678314 TEST accuracy: 0.897599995136261 Computation time:2.425 sec
・ReLU関数
TEST loss: 0.24740302562713623 TEST accuracy: 0.9282000064849854 Computation time:2.326 sec
■学習経過表示
・シグモイド関数

・ReLU関数

ReLU関数を適用した場合の方が正答率が上がりました。
特に特徴としては早い段階で学習率が十分に上がっていることが確認できます。
今回の場合では驚くほどの効果は見られないようにも思えますが、複雑になるほど差がでてくると思われます。
中間層の数を増やしてみる
ちょっとお試し。
シグモイド関数に関しては層を多層化するほど学習率が落ちやすいということが前項の導出により分かっていますので中間層の総数を変えてみました。
■最終正答率
・シグモイド関数(中間層2層)
TEST loss: 0.7661280035972595 TEST accuracy: 0.857200026512146 Computation time:2.368 sec
・シグモイド関数(中間層3層)
TEST loss: 0.9398178458213806 TEST accuracy: 0.7538999915122986 Computation time:2.525 sec
・ReLU関数(中間層2層)
TEST loss: 0.22324253618717194 TEST accuracy: 0.9355999827384949 Computation time:2.427 sec
・ReLU関数(中間層3層)
TEST loss: 0.21454575657844543 TEST accuracy: 0.9383000135421753 Computation time:2.486 sec
層の増やし方の実装が正しいか微妙な感じもします。
非常に不思議な感じもしますが、シグモイド関数に関しては層を増やすごとに正答率が落ちています。
問題設定にもよるのだと思いますが、これではディープラーニングの真価は発揮できなそうですね。
対してReLU関数では、現在の実装方法ではやや頭打ち感はあるものの層を増やすごとに正答率は上がってきていくという狙い通りの結果が確認できました。
ライブラリを使用した実装だと一度実装してしまえば変更を加えるのもかなり容易ですね。
その代わりすっ飛ばして進んでしまうと仕組みが分からず進んでしまいそうな気もしますが
次回も同様の題材を使用して工夫を加えていきます。
ーーーーーーーーーーーーー
・今回のソース
python_dev/MNIST_2.ipynb at master · wantanblog/python_dev · GitHub